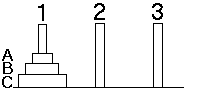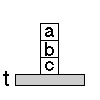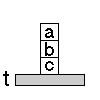Előadó: Dr. Várterész Magdolna
Példák állapottér-reprezentációra
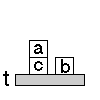
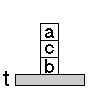
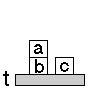
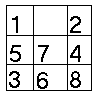
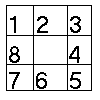
1.) 8-as játék
Feladat: egy 3´3-as
táblán számozott lapocskáink vannak, melyek közül
egy üres:
 |
|
|
 |
| |
|
|
ez a kiindulási állapot. Egy lehetséges
célállapot:
|
| |
|
| |
|
Célunk, hogy egy adott sorrendet
elérjünk úgy, hogy CSAK tologatni lehet a lapokat, méghozzá
úgy, hogy csakis az üres pozíció irányába
lehet tolni a szomszédos lapokat.
Állapottér reprezentáljuk:
Első lépés az állapottér
megadása. Fel kell deríteni, hogy mik a fontos jellemzők!
a) a számozott lapocskák
pozíciója a fontos
Ekkor a lapocskák helyzete leírható
egy számpárral (sor, oszlop). Ekkor:
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
|
(1,1)
|
(1,3)
|
(3,1)
|
(2,3)
|
(2,1)
|
(3,2)
|
(2,2)
|
(3,3)
|
(Első sor: sorszámozott lapocskák.
Alattuk: (s,o) pár, ahol a sor és az oszlop 1 és 3 között
változhat).
Ezen halmazok Descartes-szorzata rengeteg
hibás eredményt is adhat, hiszen két lapocska egyazon
helyen nem lehet (kényszerfeltétel). Egy számozott lapocskát
a mellette levő üres pozícióba lehet tolni (viszont
az üres pozíció ebből nehezen határozható
meg).
b) az a fontos, hogy az egyes pozíciókon
milyen lapok vannak
Ez a feladatunk egy másfajta állapottér-reprezentációja
lesz (hiszen mint tudjuk, egy problémához többfajta állapottér-reprezentáció
is megadható).
|
(1,1)
|
(1,2)
|
(1,3)
|
(2,1)
|
(2,2)
|
(2,3)
|
(3,1)
|
(3,2)
|
(3,3)
|
pozíció
|
|
1
|
0
|
2
|
5
|
7
|
4
|
3
|
6
|
8
|
lapocska
|
(Első sor: az egyes cellák
pozíciója. Alattuk: ezen a pozíción milyen számú
lapocska van. Az "üres lapocskát" jelöljük
0-val).
Hi,j = {0,1,2,3,4,5,6,7,8}
A Í H1,1
´ ... ´ H3,3
1 lapocska egyszerre 1 pozíción
lehet. Ezt kell majd a kényszerfeltételben megfogalmazni. Ez
már egy egyszerűbb állapotleírás.
Reprezentálás: 3´3
-as mátrix, minden elem értéke 0-tól 8-ig terjedhet.
Egyre kell vigyázni: egy érték egyszerre csak egy pozíción
lehet!
Operátorok:
- 8´4 operátor,
8´4 előfeltétel. Fel, le, jobbra,
balra tolhatom, ha fent, lent, jobb, bal oldalon üres pozíció
van.
- FEL, LE, JOBBRA, BALRA
az üres lapocskát mozgatjuk
|
FEL: ha nem a legfelső sorban van
|
| LE: ha nem a legalsóban |
| JOBBRA: ha nem jobb szélen van |
| BALRA: ha nem bal szélen van |
Megoldása: FEL, LE, JOBBRA, BALRA operátorsorozat,
amellyel a kezdőállapotból előállítható
a célállapot.
Egy problémát tehát nagyon sokféleképpen
lehet állapottér-reprezentálni.
Figyelembe kell venni az implementáció eszközöket, a
probléma bonyolultságát, stb.
2.) Hanoi tornyai
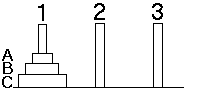 |
Feladat: az első oszlopon
lévő 3 db korongot rakjuk át úgy a harmadik
oszlopra, hogy egyszerre csak egy korongot |
| mozgathatunk, s egy korongon nem lehet
nála nagyobb korong |
| Fontos: a korongok hol vannak,
melyik oszlopon |
| |
A
|
|
B
|
|
C
|
| Állapot = |
{1,2,3}
|
´
|
{1,2,3}
|
´
|
{1,2,3} |
Ezzel megvan az állapottér. Az értékhalmaz
minden esetben ugyanaz.
Állapottér: ezen halmazok Descartes-szorzata.
Minden korong is lehet ugyanazon az oszlopon: 27 állapotból áll
(a Descartes-szorzat minden értékhármasa előfordulhat).
Egy oszlopon a korongok mindig csak felülről
lefele növekvő sorrendben helyezkedhetnek el.
Kezdőállapot: k = (1,1,1)
Célállapot: c = (3,3,3)
Operátorok:
| átrakása |
x korongnak |
| |
i. oszlopról |
| |
j. oszlopra |
| előfeltétel: |
1., az x korongnak az i. oszlopon legfelül
kell lennie |
| |
2., a j.-en nincs semmi vagy nála
nagyobb korong van |
| az operátor hatása: |
az értékhármasban
az x koronghoz tartozó i. pozíció j-re fog változni |
Tehát az előfeltételek:
- az x korong az i. rúdon legyen legfelül
all(x) = i 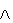 |
"y(y <x
É all(y) 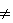
i)
|
| |
(és minden korong, ami nála
kisebb, nem lehet azon a rúdon Þ
legfelül van!) |
- a j. rúdon az x korongnál nincs kisebb
"y(y<x É
all(y) 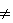 j)
j)
Hatása:
| all'(x) = j |
y 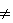 x
x  all'(y) = all(y)
all'(y) = all(y) |
| |
(a többi marad a helyén) |
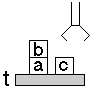
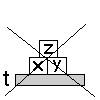
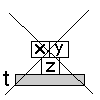
3.) Építőkocka
játék
Feladat: egy táblán, asztalon építőkockák
vannak. Van egy robotkarunk, ezzel tudunk pakolni.
Most bizonyos viszonyok lesznek fontosak: a kockák
egymáshoz ill. az asztalhoz való viszonya.
| típus: |
kocka |
| konstans: |
a,b,c,t |
(az asztal is egy speciális kocka
objektum) |
Predikátumszimbólumokat használunk
a viszonyok kifejezésére:
| RAJTA(x,y) |
x rajta van y-on |
| |
(x,y kocka típusú változó) |
| URES(x) |
x kocka teteje üres, nincs rajta semmi |
| TART(x) |
a robot tartja az x kockát |
Atomokat, atomi formulákat tudunk majd megadni,
s egy-egy állapotot ezen atomok egy-egy konjunkciójaként
lehet leírni. Literálok konjunkciója ®
állapotok megadása. Ezen konjunkciók egy-egy halmaza adja
az állapotteret.
Kényszerek:
Az asztal egyetlen más kockán sem lehet:
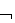 $x
RAJTA(t,x)
$x
RAJTA(t,x)
De további kényszerfeltételek is gyárthatók:
 |
|
| Egy kocka csak egy
kockán lehet rajta: |
"x"y"z(
RAJTA(z,x) RAJTA(z,y)
É (x=y) ) RAJTA(z,y)
É (x=y) ) |
| |
 |
|
| Egy kockán nem lehet 2 db kocka: |
"x"y"z(
RAJTA(x,z) RAJTA(y,z)
É (x=y)Ú(z=t) ) RAJTA(y,z)
É (x=y)Ú(z=t) ) |
| |
Továbbá:
"x( TART(x)
É x  t)
t) |
- a táblát nem tarthatja |
"x"y(
TART(x) TART(y)
É (x=y) ) TART(y)
É (x=y) ) |
- egyszerre csak egy kockát tud
tartani |
| |
|
| Kezdőállapot: |
RAJTA(a,t)  RAJTA(b,a)
RAJTA(b,a)  URES(b)
URES(b)  RAJTA(c,t)
RAJTA(c,t) 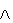 URES(c)
URES(c) |
| Célállapot: |
RAJTA(c,t) 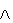 RAJTA(b,c)
RAJTA(b,c) 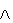 RAJTA(a,b)
RAJTA(a,b) 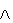 URES(a)
URES(a) |
Most 1 célállapot van, de lehetne célállapotok
halmaza is. Pl.: "a" valamelyik kockán legyen:
Ekkor a feltétel: $y(
y 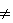 t
t
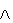 RAJTA(a,y)
)
RAJTA(a,y)
)
Mozgás:
| a robot felemel egy kockát ®
állapotváltozás |
ü |
|
| |
ý |
lehetne ez a két operátor
|
| a robot lerak egy kockát ®
állapotváltozás |
þ |
|
| |
|
| fel: |
x kockát emeli fel a robot |
| |
előfeltétel: |
(x 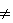 t) t)
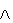 URES(x) URES(x)
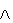 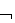 $y
TART(y) $y
TART(y) |
| |
|
(ez az x kocka nem az asztal, nincs rajta
semmi, és a robot
nem tart semmit) |
| |
hatása: |
1. Megkeressük azt az y-t, melyen
RAJTA(x,y).
Erről kell majd felemelni. |
| |
|
2. Töröljük a RAJTA(x,y)
-t, URES(x) -et is (mert azt már fogja). |
| |
|
3. Ha y 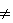 t
® hozzáadjuk az állapotleíróhoz
az URES(y) -t t
® hozzáadjuk az állapotleíróhoz
az URES(y) -t
(ez egy atom) |
| |
|
4. Hozzáadjuk TART(x) -et. |
| |
|
|
| le: |
x kockát rátesszük
y-ra |
| |
előfeltétel: |
TART(x) 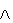 (
(y=t) Ú (URES(y)) ) (
(y=t) Ú (URES(y)) ) |
| |
hatása: |
1. TART(x) -et töröljük |
| |
|
2. RAJTA(x,y) -t hozzáfűzzük, s
ha y 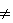 t,
akkor töröl URES(y) t,
akkor töröl URES(y) |
| |
|
3. URES(x) hozzáadása |
4.) Utazó ügynök probléma
Feladat: egy titkosügynöknek egy listán
lévő összes várost be kell járnia, s miután
küldetését teljesítette, vissza kell térnie
a kiindulási városba.
Az utaknak költsége van. Probléma: olcsó
körút, rövid körút. Tervezzük meg ezeket.
Egy lehetséges megoldás, ha felsoroljuk az
összes lehetséges esetet, s kiszámoljuk a legrövidebbet,
legolcsóbbat. "n" darab város esetén ez azonban
n! (n faktoriális). Ha "n" nő, akkor n! nagyon gyorsan
nő! Pl. 50 város esetén ez az érték olyan
nagy, hogy gyakorlatilag megoldhatatlan. Ez egy tipikus mesterséges intelligencia
probléma.
Általában jó megoldást szoktunk keresni,
nem optimálisat.
Hogyan lehetne ezt állapottér-reprezentálni?
Felsoroljuk a városokat:
| |
type varos = (A,B,C,D,E,N); |
| |
var alltip: array [1..6]
of varos; |
| |
|
| kezdőállapot: |
(A,A,N,N,N,N) |
| célállapot: |
(A,.......,A) |
Operátorok:
| beszúrás: |
X város után beszúrja
Y várost |
| |
előfeltétele:
X-nek már, Y-nak még nem szabad a körútban szerepelnie |