Előadó: Dr. Várterész Magdolna

2. Problémareprezentációs technikák, megoldáskereső módszerek

A problémát ahhoz, hogy kezelni tudjuk, valamilyen módon meg kell adni, le kell írni. Milyen problémákkal fogunk foglalkozni? Olyanokkal, amelyek megoldásához nincs ismert megoldó-algoritmus, képlet. Tapasztalat, tudás segítségével oldjuk meg a problémát.

Ezen problémák számítógépes megoldásához keresünk algoritmusokat.

Első feladatunk a probléma leírása, reprezentálása. Háromféle reprezentációs eszköz:

  1. Állapottér-reprezentáció
  2. Probléma-redukció
  3. Logikai alapú (elsőrendű nyelvvel)

2.1. Állapottér-reprezentáció

2.1.1. Állapottér

Legyen adott egy p probléma. A probléma állapottér-reprezentációjának elkészítéséhez meg kell vizsgálni, hogy melyek p világában azok a tulajdonságok, jellemzők, amelyek fontosak számunkra. Tegyük fel, hogy n ³1 ilyen jellemzőt találtunk. Minden egyes jellemző p világát különböző értékekkel jellemzi (pl.: életkor: 20; szín: fekete; stb.). Ha a világ n különböző jellemzőjét rendre a h1,...,hn értékek jellemzik, akkor azt mondjuk, hogy a (h1,...,hn) érték n-essel azonosított állapotban van p világa.

Jelölje az i. jellemző által felvehető értékek halmazát Hi (i = 1,...,n). Ekkor p világának állapotai elemei a H1´...´Hn halmaznak. Az állapotok halmazát állapottérnek nevezzük, és A-val jelöljük.

AÍH1´...´Hn Lehet, hogy a világunkban a jellemzőkhöz tartozó
bizonyos értékek egyszerre nem léphetnek fel, tehát az állapottér az értékhalmazok Descartes-szorzatának csupán valamely részhalmaza.

Kényszerfeltétel: az a feltétel, ami az állapotteret kijelöli az értékhalmazok Descartes-
szorzatából
jelölése: kf(a) ,mely igaz, ha a állapot, egyébként hamis

A = { a | aÎH1´...´Hn és kf(a) }

Problémafelvetés:

  1. Az állapottér mely állapotában vagyunk kezdetben: kezdőállapot. Ez is egy érték n-es, s kitüntetett szerepe van.
    k Î A
  2. cél, hova akarunk eljutni. cÎC Í A célállapotok halmaza
    a feladat általában: a kezdőállapotból jussunk el a megfelelő célállapotba

    Megadása kétféleképpen történhet:

    1. explicit módon, felsorolással. Egy- vagy többféle állapot is lehet. Több állapot esetén ez nehézkes lehet. Ilyenkor:
    2. implicit módon, célfeltételek megadásával: C = { a | aÎA, cf(a) }

  3. Ahhoz, hogy eljussunk a célállapotba: meg kell változtatni az állapotot.

    o Î O o: A ® A
    állapottérből állapottérbe képező függvény. Az állapot megváltoztatásáért felelős.
    o: operátor
    O: operátorok halmaza


    Természetesen nem minden operátor alkalmazható minden esetben. Meg kell adni a pontos értelmezési tartományt: operátor-alkalmazási előfeltételek. (minden egyes operátorhoz hozzátartoznak)

    dom(o) = { a | aÎA, efo(a) } , ahol efo(a) azon előfeltétel, mely megmondja,
      hogy az adott állapoton értelmezhető-e
      a kérdéses operátor
    efo(a) esetén o(a) = a' ÎA

     

Definíció: A p problémát leírtuk állapottér-reprezentációval, ha megadtuk a p = <A,k,C,O> négyest, ahol

p = <A,k,C,O> ilyenkor megadtuk a p probléma állapottér-reprezentációját
Több reprezentáció is megadható ugyanarra a feladatra.

Mit jelent ennek az implementálása?

  1. egyrészt meg kell adni az értékhalmazokba tartozó értékek típusát
    kényszerfeltételek: az értékhalmazból mely értékek valódi állapotok

    Boolean függvények: a formális paraméterben vár egy érték n-est, s egy logikai értéket ad vissza (igaz v. hamis)

  2. kezdőállapot. Állapot típusú konstans
  3. célállapotok. Megadása történhat:
    1. célfeltételekkel: boolean, kap egy állapotot, s visszaad egy logikai értéket
    2. konstansokkal
  4. operátorok: függvények, eljárások. Kap egy állapotot, s egy új állapotot állít elő.

    Minden egyes operátorhoz tartozik egy előfeltétel is (boolean típusú függvény).


Kezdőállapotból mikor, melyik operátor alkalmazásával tudunk eljutni a célállapotba?

Az aÎA -ból az a'ÎA közvetlenül elérhető, ha van olyan oÎO: efo(a) és o(a) = a'

Az aÎA -ból az a'ÎA elérhető, ha van olyan a1,...,anÎA (állapotsorozat), hogy a=a1, a'=an és ai-ből ai+1 közvetlenül elérhető.
(a a kezdőállapot, a' a célállapot, i=1,...,n-1).
Ilyenkor van egy operátorsorozat, ami ezt az elérést lehetővé teszi: o1,o2,...,on-1

Egy állapottér-reprezentált probléma megoldható, ha a kezdőállapotból elérhető valamelyik célállapot.

Mi a megoldása? Az az operátorsorozat, amely ezt az elérést lehetővé tette. (De lehet több megoldása is függetlenül attól, hogy hány célállapot van).

A feladat lehet egy vagy több megoldás előállítása. Célunk: minősítés alapján jó megoldás keresése, azaz a megoldások között különbséget teszünk, pl.: költség.

Költség: az operátorok alkalmazása költségbe kerülhet.
 

(egy operátor használata egy állapotra ® ennek van költsége)

ez lehet mindig azonos, vagy függhet attól, hogy melyik állapotra alkalmazzuk

r(o,a) d > 0 (pozitív alsó korlátja van, aminél a költség nem lehet kisebb)

r(o,a) -ban o az operátor, a pedig, hogy milyen állapotban alkalmazható
Ha r(o,a) 1, akkor ez az alkalmazott operátorok számát fogja jelölni

Az operátoroknál meg kell adni az operátorok költségét (függvénnyel, eljárással megadható).

Mi a megoldás költsége?

Az operátorsorozat operátorainak költségösszege:  

A különböző megoldásokat így össze lehet hasonlítani!
Optimális költség: (olcsó), legolcsóbb megoldás keresése.

Feladat: megoldást kell előállítani. Nem tudom megmondani, hogy mikor melyik operátort alkalmazzuk. A megoldást keresni kell.

Példák

2.1.2. Szemléltetése

Legyen a p probléma az <A,k,C,O> állapottér-reprezentációval megadva. Szemléltessük egy gráffal ezt a probléma-leírást a következőképpen: az állapottér állapotait csúcsokkal szemléltetjük, különböző állapotokat különböző csúcsokkal.
A kitüntetett állapotokat, mint a kezdő- és célállapotokat a csúcsok között is kitüntetjük, a kezdőállapotot szemléltető csúcsot startcsúcsnak, a célállapotokat szemléltető csúcsokat terminális csúcsoknak nevezzük.

Minden aÎA -t szemléltető n csúcsból irányított élt húzunk az a'ÎA -t szemléltető n' csúcsba, ha a-ból közvetlenül elérhető a'.

Így egy <N,s,T,E> gráfot kapunk, ahol
N
 a csúcsok halmaza
s
 a start csúcs
T
 a terminális csúcsok halmaza
E
 az élek halmaza

Ezt a gráfot a p probléma <A,k,C,O> állapottér-reprezentációjához tartozó állapottér-gráfjának vagy reprezentációs gráfjának nevezzük.

Fogalmak:

irányított utak: Pontosan akkor vezet az állapottérgráfban az n csúcsból
  az n' csúcsba irányított út, ha az n által szemléltetett állapotból az n' által szemléltetett állapot elérhető.
megoldható: van a start csúcsból valamelyik terminálisba vezető irányított út
megoldás: pontosan ez ( ) az irányított út szemlélteti a megoldást
költség:
r(o,a)
 Az irányított élekhez rendelhetők költségek, hiszen azok
    az operátorok alkalmazását szemléltetik
irányított út költsége:   a benne szereplő élek költségösszege
    r(n,n') d > 0
Egy probléma
megoldásának keresése:		 a probléma-reprezentációs gráfban fogunk utat keresni a start csúcsból a terminálisba

Egy gráfban annál könnyebb keresni, minél egyszerűbb annak a felépítése, ill. minél kisebb. Ez többféleképpen is elérhető:

1. csúcsok számának csökkentése
ü
  
  (állapotok számának csökkentése)
ç
2. egy (1) csúcsból kiinduló élek számának csökkentése
ý
 állapottér-reprezentációval van kapcsolatban
ç
  (operátorok ügyes, alkalmas megválasztása)
þ
  
3. fává egyenesítés    
  A reprezentációs gráfban lehet hurok:
  illetve kör:
    ezeket kell kiegyenesíteni!

Hurok kiegyenesítése:
®
 

Ugyanazt az állapotot két különböző csúccsal reprezentáljuk! Gond: nő a fa terjedelme!

Kör kiegyenesítése:
®
 
Gond: a kör kiegyenesítése végtelen szerkezettel jár együtt. Mérlegelni kell, hogy a fává egyenesítés megéri-e.

 

Példák (néhány probléma gráfreprezentációja):

1.) 8-as játék:

Minden él mellett van egy párhuzamos visszairányuló él. Ilyenkor használhatunk egy irányítás nélküli élet is.
           
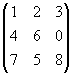Megoldás!!!

Ez egy olyan probléma, ahol a fává egyenesítéssel érdemes élni.

2.) Utazó ügynök probléma

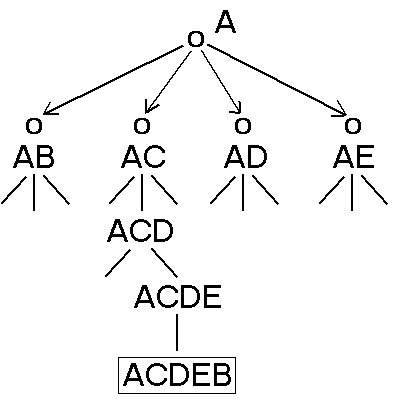
Ez egy fa-gráf, s minden egyes útjának végén (a levél) terminális csúcs. Az utak közül az optimálisat kellene kiválasztani.

Vissza a lap tetejére