Kompression - Das inverse Problem

Fraktale Kompression ist das inverse Problem zu den IFSen: Zu einem gegebenen Bild soll eine Funktion gefunden werden, die bei Iteration das Bild möglichst gut annähert. Dazu muß im Bild nach Selbstähnlichkeiten gesucht werden, also nach Teilbildern, die anderen Teilbildern möglichst ähnlich sind.

Für dieses Problem reichen aber die Möglichkeiten der normalen MRCM nicht aus. Wir erweitern sie daher wie folgt.

Partitionierte MRCMs

Die Kopiermaschine von oben wird um folgende Einstellregler erweitert:

(Bildquelle: [BH93])

Damit ergeben sich Transformationen der Form:


w(x,y,z)= Matr(a b 0 / c d 0 / 0 0 s) (x y z) + (e f 0)


wobei z = f(x,y), s Kontrast und o Helligkeit.

Anpassung von Helligkeit und Kontrast

Die Einstellungen für Kontrast und Helligkeit werden notwendig, um die Bildteile besser aneinander anzupassen. Bei der Suche nach Selbstähnlichkeiten werden zunächst die beiden zu vergleichenden Bildausschnitte mittels der Methode der kleinsten Quadrate auf das gleiche Helligkeits- und Kontrastniveau gebracht, um so eine höhere Ähnlichkeit und damit bessere Resultate zu erreichen.

Die Anpassung der Bilder f und g entspricht der Minimierung von R = Summe (s f(x,y) + o - g(x,y)) ^2
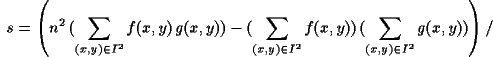
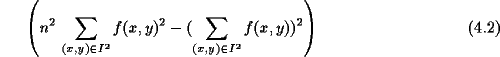
R wird minimal, wenn die partiellen Ableitungen nach s bzw. o null sind. Dies ist der Fall, wenn s = komplizierte Formel s = komplizierte Formel
und
o = (Summe g(x,y) - s Summe f(x,y)) / n^2

Abstandsfunktion für Bilder

Als Abstand zweier Bilder f, g kann prinzipiell jede Funktion verwendet werden, die die Bedingungen einer Metrik erfüllt, z.B.:

Partitionierungsverfahren

Da es unendlich viele Transformationen gibt, müssen die erlaubten Transformationen zunächst eingeschränkt werden. Dazu wird das Bild in Teilbereiche partitioniert, die dann für die Vergleiche verwendet werden. Für jede Partition kann dann in allen größeren Partitionen bzw. Kombinationen von Partitionen nach größter Ähnlichkeit gesucht werden.

Zur Partitionierung gibt es verschiedene Verfahren:

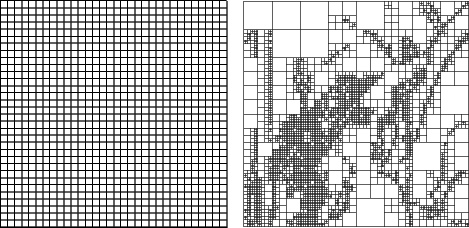
(Bildquelle für Quadtree-, HV- und Triangulare Partitionierung der Lena: [Fis92])

Ein einfaches Beispiel

Mit diesen Voraussetzungen können wir nun einen vollständigen Komprimierungsalgorithmus beschreiben, um ein Bild mit 256 Graustufen und einer Auflösung von 256 x 256 Punkten zu komprimieren.

Wir benutzen als Partitionierungsverfahren die Quadrate fester Größe, wobei die Größe der Quadrate 8 x 8 Punkte sei. Damit wird das Bild in 1024 kleine Quadrate partitioniert, die wir mit R1, ..., R1024 bezeichnen. Das Bild wird außerdem in die 241 x 241 = 58.081 (überlappenden) 16 x 16 Quadrate aufgeteilt (bezeichnet als Menge D).

Durch die Partitionierung in Quadrate sind nur noch Drehungen um 90 Grad und Spiegelungen an der X- oder Y-Achse erlaubt. Außerdem ist der Verkleinerungsfaktor auf 25% festgelegt. Damit gibt es nur noch 8 mögliche Transformationen.

Nun sucht man für jedes Ri das Di in D, das ihm am ähnlichsten sieht. Dazu wird jeweils zunächst das Ri auf die Größe des Di gebracht, d.h. es werden einfach aus jedem Pixel 4 Pixel gemacht. Dann werden mit Hilfe der oben angegebenen Formeln die Faktoren für die Helligkeits- und Kontrastanpassung der beiden Bilder ermittelt und auf eines der Bilder angewendet. Dann kann für jede der 8 möglichen Transformationen der Abstand (z.B. mit einer der o.a. Formeln) des einen Bildes zum transformierten anderen Bild berechnet werden. Von allen Di wird dann das Di genommen, das dem Ri am ähnlichsten ist (mit einer bestimmten Transformation), und dieses wird abgespeichert.

Dies wird für alle Partitionen wiederholt, somit sind 1.024 mal 58.081 mal 8 = 475.799.552 Transformationen und Bildvergleiche notwendig, hinzu kommen 1.024 mal 58.081 = 59.474.944 Helligkeits- und Kontrastanpassungen. Der Aufwand ist also trotz der vereinfachten Voraussetzungen (relativ kleines Graustufenbild, Verwendung des einfachsten Partitionierungsverfahrens, starke Einschr"ankung der erlaubten Quellbereiche) erheblich.

Die Quelldatei hat eine Größe von 512 mal 512 = 262.144 Byte, die komprimierte Datei besteht aus 1024 Transformationen mit jeweils 16 Bit für den Quellbereich, 3 Bit für die Transformation (da nur 8 verschiedene erlaubt sind) und 12 Bit für die Helligkeits- und Kontrastanpassung, also insgesamt 31 Bit. Sie hat damit eine Dateigröße von ca. 8.192 Byte, was einer Komprimierung um den Faktor 16,5 oder auf 6,1% entspricht.

Hier die Dekomprimierungsstufen eines mit genau diesen Parametern komprimierten Lena-Bildes: Ursprungsbild, 1. Iteration, 2. Iteration und 10. Iteration. (Bildquelle: [Fis92])

Und hier noch einmal der allgemeine Kompressions-Algorithmus: 

+--------------------------------------------------------+
| fuer alle Partitionen Ri                               |
|  +-----------------------------------------------------+
|  | minimum:=MAXINT                                     |
|  +-----------------------------------------------------+
|  | fuer alle groesseren Bildbereiche D                 |
|  |  +--------------------------------------------------+
|  |  | Passe Ri und D in Groesse und Helligkeit an      |
|  |  +--------------------------------------------------+
|  |  | fuer alle moeglichen Transformationen Dt von D   |
|  |  |  +-----------------------------------------------+
|  |  |  | berechne den Abstand zwischen Ri und Dt       |
|  |  |  +-----------------------------------------------+
|  |  |  |              Abstand < minimum ?              |
|  |  |  | ja                                       nein |
|  |  |  +--------------------------------+--------------+
|  |  |  | minimum:=Abstand               |              |
|  |  |  +--------------------------------+              |
|  |  |  | merke das D mit Transformation |              |
|  |  |  | und Helligkeit/Kontrast        |              |
|  +--+--+--------------------------------+--------------+
|  | speichere das gemerkte D mit Trafo. und Hell/Kontr. |
+--+-----------------------------------------------------+
Bei Quadtree-, HV- und Triangularer Partitionierung wird so vorgegangen, daß zunächst bis zu einer gewissen Maximalgröße partitioniert wird. Dann wird geprüft, ob der minimale Abstand zu einem Quellbild bereits eine anzugebende Schranke (als Maß für die gewünschte Kompressionsrate bzw. Bildqualität) unterschritten hat. Wenn nicht, wird das Bild weiter partitioniert; sonst wird die Transformation gespeichert und die Partitionierung (in diesem Ast) abgebrochen.

Speicherung des komprimierten Bildes

Allgemein müßten für jede Transformation die 8 Werte aus der o.a. Formel gespeichert werden. Je nach verwendetem Partitionierungsverfahren können diese Werte jedoch durch andere, kürzer darstellbare Werte ersetzt werden. Zum Beispiel könnte bei Quadtree mit jeweils einem Bit angegeben werden, ob das jeweilige Quadrat weiter unterteilt wird oder nicht. Beim HV-Verfahren reicht es, zusätzlich jeweils einen Offset für die Teilungsstelle anzugeben der ziemlich schnell recht kleine Werte annimmt.

Zusätzlich muß für jede Transformation auch noch gespeichert werden, auf welches Teilbild sich die Transformation bezieht, d.h. es müssen je nach Partitionierungsverfahren noch einmal eine Zahl oder ein bis drei Koordinaten gespeichert werden.

Insgesamt kommt man erfahrungsgemäß im Durchschnitt mit ca. 31 Bit pro Partition aus. Die Anzahl der Transformationen, die gespeichert werden müssen, hängt ab vom Partitionierungsverfahren, von der Feinheit der Partitionierung und damit von der angestrebten Bildqualität.

Komprimierung von Farbbildern

Bisher wurde nur die Behandlung von Graustufenbildern angesprochen. Um nun ein Farbbild zu komprimieren, wird das gleiche Verfahren wie für Graubilder einfach auf jeden Farbanteil des Farbbildes angewendet (z.B. auf den Rot-, Grün- und Blauanteil). Bei der Dekomprimierung wird dann jeder Anteil getrennt dekomprimiert und alles zum Schluß wieder zusammengesetzt.

nächster Teil: Vergleich zu JPEG und Wavelets

Hauptseite fraktale Kompression

voriger Teil: IFS

Jochen Quante