
Előadó: Dr. Várterész Magdolna
3. Kétszemélyes, teljes információjú játékok
A játékokat két nagy csoportba tudjuk sorolni:

Előadó: Dr. Várterész Magdolna
3. Kétszemélyes, teljes információjú játékok
A játékokat két nagy csoportba tudjuk sorolni:
Neumann János maga is foglalkozott ezzel. Harsányi János 1994-ben közgazdasági Nobel-díjat kapott; a játékelmélet az ő nevéhez fűződik.
Stratégiai játékok osztályozása:
| résztvevők száma: | 2,3,...,n személyes játékok |
| (néha a véletlent is személynek veszik) | |
| véges játékok: | olyan stratégiai játékok, amelyben minden állásban véges sok |
| szabályos lépés közül lehet választani, s véges sok lépés után véget ér | |
| zérusösszegű: | ha nyeremények + veszteségek = 0 |
| (beszélhetünk nem zérusösszegű stratégiai játékokról is) | |
| véletlen szerepe: | 1. sztochasztikus (pl. bridge) |
| 2. determinisztikus (pl. sakk) | |
| teljes információjú: | tudom, hogy a másik mit lépett. A játékosok a játékkal |
| kapcsolatos összes információt ismerik, s felváltva lépnek. |
| Leírás: | játékszabályok megadása |
| Milyen játékállások fordulhatnak elő, az egyes állásokban
milyen szabályos lépések vannak, mik ezeknek az előfeltétele. Célfeltétel: mikor kell befejezni, milyen állásban, s ekkor kit kell győztesnek kikiáltani. |
A kétszemélyes játékot is le kell írni. Ehhez a következő leírást alkalmazzuk:
3.2. A játékok reprezentációja és a reprezentáció szemléltetése
H legyen a játék állásainak a halmaza, {A, B} a két játékos.
| All = { (h, x) | h |
- ez az állapottér, ahol x azt jelzi, hogy ki következik |
Kezdőállapot:
| k = (i, I) | ,ahol i |
Végállapot:
| V = { (h, x) | h |
megállapodás kérdése, hogy x |
| nyertes vagy vesztes |
Lépés:
l: H ![]() H
H
| előfeltétell(h) | az egyes lépésekhez előfeltételek is tartoznak |
Operátorok:
O = { o: (h, x) ® (h', x') | l: h ® h', előfeltétell(h) teljesül, h,h' Î H és x' = x ellenfele }
A játék állásait egy reprezentációs gráffal tudjuk szemléltetni. A reprezentációs gráf egy játékgráf:
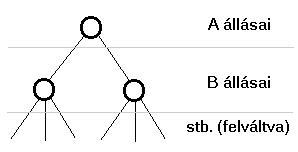
Véges játék esetén véges a gráf is. Minden
út benne véges.
Körök: a játékszabályok ezt általában nem engedik, vagy adnak rá valami korlátozást
(a köröket fává egyenesítéssel is fel lehet oldani).
A start csúcsból egy levélbe vezető út: egy
lehetséges játszma.
Egy játékos számára hogyan lehetne egy teret adni, ami
befolyásolná a játék kimenetét? Stratégia. Ez mindig egy (1) játékoshoz
tartozik. Minden, a játék során előforduló állapotban amikor ő következik a
stratégia megmondja, hogy mit lépjen. A stratégia tehát egy döntés.
Jó a stratégia, ha minden állapotra van terv, bármit is
lép az ellenfél.
Lehetséges hiperutak: a játékos különböző stratégiái. Ahány különböző hiperút,
annyi különböző lehetséges stratégia a játékos számára.
Gyűjtsük össze a játék során előfordulható összes állapotot:
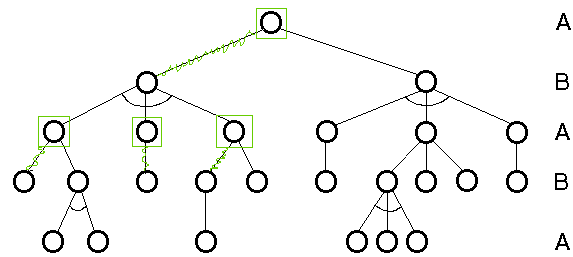
Tegyük fel, hogy például A szeretne
nyerni. Ekkor a start állapotnak szerepelnie kell a stratégiában.
Menjünk tovább a zölddel jelölt részen. B viszont (az ellenfél) bármit
léphet, ezért az ÖSSZES olyan állapotnak is szerepelnie kell a stratégiában
amelyet B léphet, hiszen az ellenfél minden válaszlépésére reagálni kell
tudni!
Ahol A következik lépni: választunk a szabályos lépések közül. VAGY lépések vannak, lehet választani. B lépései ÉS élek. Ha B lép, akkor a stratégiába fel kell venni mindazon állapotokat, ahova B léphet.
|
|
Át kell alakítani a játékfát az ADOTT játékos alapján ÉS-VAGY gráffá. Ebben kell hiperutakat keresni! Az adott játékosnál VAGY élek lesznek, az ellenfélnél pedig ÉS élek. |
Hogyan választunk: úgy, hogy a játék kimenetele lehetőleg nyeréssel végződjön, ne veszítsünk.
Nyerő stratégia: a stratégiával játszva
a másik játékos lépéseitől függetlenül garantáltan nyerünk! Ha a levélelemek
mind nyerőállások, akkor a stratégia nyerő.
Feladat: a stratégiák közül válasszunk nyerő stratégiát.
3.4. Adott állásban a következő lépés kiválasztásának módszerei
Minden kétszemélyes, teljes információjú játék
esetén az egyik (és csakis az egyik) játékos számára garantáltan van nyerő stratégia.
Ha van, akkor több is lehet.
Kérdés: melyik játékos számára lesz?
Az állítás csupán azt garantálja, hogy az egyiknek van nyerő stratégiája.
Bizonyítása konstruktív módon történik, s ehhez az egész játékfát elő kell állítani:
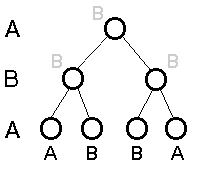 |
A leveleket megcímkézzük azalapján, hogy ott ki nyert. Ezután
visszafelé haladunk (itt középső szint), s megnézzük, hogy ki lép (itt B).
Mivel B tud úgy lépni innen, hogy ő nyerjen, ezért B-t írunk be (szürkével
jelölve). Mint látható, ez egy B nyerő játék. A start csúcs
címkéje határozza meg, hogy kinek van nyerő stratégiája. Ez megkonstruálja
a nyerő játékost, s a nyerő stratégiát is. Címkemódszer. A címke jelöli,
hogy az adott állásból kinek van nyerő stratégiája. |
Az előbbi címkemódszerrel akkor van gond, ha túl nagy a játékfa (nem tudjuk előállítani), s így explicit módon nem tudjuk meghatározni hogy ki nyer. Ekkor használjuk a következő módszerek egyikét:
Nem építjük fel az adott állásban a teljes játékfát (pl. nem tudjuk, mert olyan nagy lenne).
Amit tehetünk: néhány lépésre előre kombinálunk. Az adott állásból kiinduló játékfának csak egy részét állítjuk elő. A kialakuló állások (levélelemek) nem végállások, de mégis valahogy minősíteni kellene őket, hogy tudjunk választani.
Valamilyen heurisztikára lesz szükség, amely
megmondja, hogy az adott játékos számára az adott állás mennyire jó, mennyire
ígéretes. Minél jobb az állás, annál nagyobb értéket rendelünk hozzá. Döntetlen:
0 körüli érték.
Ha az ellenfél számára jobb: negatív érték.
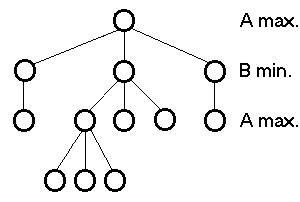
Az azonos szinten lévő levélelemeket kiértékeljük
(heurisztika). Az ősöknél ezt vesszük figyelembe, ill. azt, hogy ki következik
lépni.
| Ha A következik: | a legnagyobb értékű gyermeket fogjuk választani |
| (nekünk az a legjobb) | |
| Ha B következik: | a legkisebb értékűt választjuk |
| (ez B-nek a legjobb, ezért úgy számítunk, hogy ő azt fogja lépni, ami neki a legjobb) |
Ez a módszer az alapja minden kétszemélyes játékkal kapcsolatos tanácsadásnak!
Egy állás kiértékelőfüggvénye az egyik játékos
szempontjából értékeli ki az állásokat. Amennyire jó nekünk egy állás, annyira
rossz az ellenfélnek (és fordítva).
B számára egy állás heurisztikája pontosan az ellentetje az A
heurisztikájának.
-hA(n) = hB(n)
Nem kell szintről-szintre megvizsgálni, hogy ki következik! Levélszinten az ellenfél szerinti kiértékelőfüggvényeket adjuk meg. Ez a játékos pontosan a szülő szint ellenfele. A szülő szinten a lenti értékek az ellentettjére változnak, s ezek közül a maximumot vesszük.
A módszer előnye: nem kell egyik szinten minimumot, másikon maximumot venni. Eredménye amúgy azonos az előző módszerével. Mindig a maximumot kell venni.
Generálás közben fog kiderülni, hogy mekkora
részlet kell.
Amint van a szülőnek gyermeke, a szülő pontos értékének alsó vagy felső becslését
meg tudjuk adni.
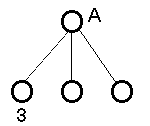
| Max. szülő |
alsó becslését tudjuk megadni a végleges értéknek |
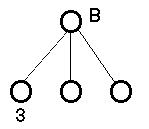
| Min. szülő |
felső becslését tudjuk megadni a végleges értéknek |
 |
 |
|
a csúcs értéke legalább 3 lesz
|
a csúcs értéke legfeljebb 3 lesz
|
Lehet, hogy még nem állítottuk elő az összes gyermeket, de már tudunk valamit mondani a szülőről.
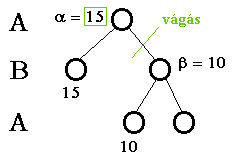 |
A zölddel jelölt résznél vágunk, mivel azt a részt már nem kell előállítani, hiszen már biztos, hogy nem fog "beleszólni" a felette lévő részbe.
|
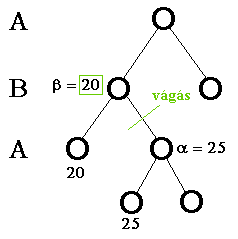 |
A zölddel jelölt résznél vágunk, mivel az az alatti rész végleges, pontos értékének a kiszámítása már biztos hogy nem fogja módosítani az eredményt.
|
Ez a módszer is ugyanazt a javaslatot eredményezi,
mint a mini-max módszer.
Előnye: csökken a játékfa mérete, mert bizonyos részeket nem kell előállítani.
| - ha ez teljesül, akkor lehet vágni |