Előadó: Dr. Várterész Magdolna

2.2.2.2.4. A-algoritmusok

 

a) "alap" A-algoritmus

optimális keresés esetén: g(s) = 0
  g(m) = g(n) + k(n,m)
    ,ahol (n,m) E, ill. k(n,m) d > 0


 

best-first: h(m) 0  
  h(t) = 0 , ha t T
  h(m) = , ha m-ből nem érhető el egyetlen
      terminális sem

 

 

 

Ötlet: ötvözzük a kettőt!

f(m) = g(m) + h(m) ez lesz a kiértékelő függvény, azaz a start-ból m-en keresztül
  valamilyen terminálisba való jutás becsült költsége


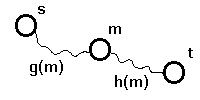
Nyilvántartja az m-ig vezető út költségét, ill. az m-ből a t-be vezető út becsült költségét.

g*(m) a start-ból m-be jutás optimális költsége
  g(m) g*(m)
h*(m) m-ből milyen költséggel juthatunk legolcsóbban célba?
  célbajutás optimális költsége
  h(m) h*(m) ,vagyis a becslés közelíti ezt az opt. értéket
f*(m) start-ból m-en keresztül a célbajutás optimális költsége
  f*(m) = g*(m) + h*(m) ,elméleti érték, kiszámítani nem tudjuk
  f(m) f*(m) , f*(m) -et szeretnénk közelíteni
f*(s) optimális megoldás költsége
  start-on keresztül a legolcsóbb célbajutás költsége
  f*(s) = h*(s) (hiszen g(s) = g*(s) = 0)

 


 

Működése: ezt az értéket fogjuk származtatni

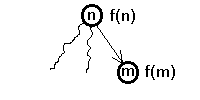 f(n) = g(n) + h(n)
g(n) = f(n) - h(n)
 
f(m) = g(m) + h(m) = g(n) + k(n,m) + h(m) =
= f(n) - h(n) + k(n,m) + h(m)
   

 


Kiterjesztésre mindig a legkisebb f(m) -űt kell kiválasztani!
Hátra és előre is tekintünk! Összességében a legolcsóbbat terjesztjük ki.

Kiterjesztésre kiválasztani: a legkisebb kiértékelőfüggvény-értékű nyílt csúcsot

1. m még nem szerepelt a keresőgráfban
  m-et felfűzzük a keresőgráfban nyílt csúcsként (n-re visszamutató pointer)
  f(m) = f(n) - h(n) + k(n,m) + h(m)
2. m szerepelt már a keresőgráfban
  a)   b)
 
 
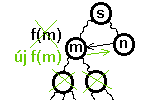  m-et feltártuk már, de még nem léptünk tovább (azaz nyílt csúcsként szerepel)   Zárt csúcsok problémája: m-ből egyszer már továbbmentünk. Amennyivel csökkent f(m) értéke, annyival kell csökkenteni az
  Ha találunk hozzá egy kisebb   egész részgráf csúcsainak a költségét.
költségű utat, akkor tároljuk azt le. Fel kell újítani!
Visszamutató nyíl n-re.  


 

Zárt csúcsok problémája:
1.
 járjuk be a rész-keresőgráfot, s frissítsünk.
 
Gond: visszamutatókat használtunk, nem
 
előremutatókat. (Reprezentációs változtatás).
 
2.
 bízzuk a dolgot az A-algoritmusra. Az m zárt csúcsból
 
csináljunk nyílt csúcsot, s ekkor ez olyan, mintha a rész-
 
gráfot még NEM jártuk volna be. Az újrabejáráskor
 
lesz korrekció!
 
3.
 megelőzés. Az optimális kereső olyan volt, hogy mikorra
 
egy csúcs zárt lett, akkor már nem található hozzá
 
vezető kisebb költségű út. Vagyis az opt. keresőnél
 
nincs ilyen gond.


 

Az optimális keresés egy speciális A-algoritmus, ahol h(n) = 0, vagyis nem számítunk heurisztikát.
Kérdés: heurisztikával rendelkező A-algoritmus esetében működik-e?
A válasz: igen, a heurisztikának kell olyannak lennie.

A vezérlő működése:
 
1. az adatbázis inicializálása: start csúcs, nyílttá tesszük
  kiértékelő-függvény megállapítása
2. van-e nyílt csúcs?      
  nincs: sikertelen a keresés
  van: kiválasztjuk a legkisebb kiértékelőfüggvényű nyílt csúcsot.
    Teszteljük: célcsúcs?
    igen: jó, vége
    nem: kiterjesztjük. Ha egy gyermeke még nem
      szerepelt a keresőgráfban: felvesszük, pointer vissza, kiértékelő-függvény kiszámítása a szülő segítségével.
Ha szerepelt már: megnézzük, hogy a hozzá vezető új út, vagy a már nyilvántartott (régi) út költsége-e kisebb? Ha az új út költsége (amit az új szülő alapján számítunk) kisebb: akkor van teendő, különben nincs.
Ha az új út költsége kisebb: ha ez nyílt, akkor a visszamutatót átállítjuk az új szülőre, s regisztráljuk az új kiértékelő-függvényt. Ha zárt, akkor visszaminősítjük nyílt csúccsá, átírjuk a visszamutatót és a kiértékelő-függvényt.
Az épp kiterjesztett csúcsból zárt csúcs lesz.
         

 


Elvárások: tetszőleges reprezentációs gráf esetén ha van megoldás: megoldása a terminál véges sok lépésben.
Felismeri véges esetben, ha nincs megoldás.

Az optimális kereső is ilyesmi tulajdonságokkal bír, az egy speciális A-algoritmus, a szélességi pedig egy speciális optimális keresés.

1. lemma: az A-algoritmus működése során bármely nyílt csúcs véges sok lépés megtétele után kiterjesztésre kerül, hacsak közben az algoritmus terminális csúcs megtalálásával nem terminál.

2. lemma: az A-alg. terminálása előtt mindig van az optimális útnak eleme a nyílt csúcsok között.

Állítás: az A-algoritmus megoldással rendelkező reprezentációs gráf esetén véges sok lépésben terminálissal terminál.

 

Bizonyítás (1. lemma):

legyen
r
 a keresőgráf egy csúcsa
 
f(r)
 kiértékelő-függvény (az r csúcsig vezető út költsége + heurisztika)

 


f(r) = g(r) + h(r) g(r) g*(r)

A nyilvántartott, r-ig vezető út vagy az optimális, vagy sem, azaz mint az odavezető opt. út.

d*(r) r-ig vezető optimélis út éleinek a száma
g*(r) optimális út költsége
  g*(r) d*(r) × d
összesen d*(r) él van f(r) d*(r) × d "r esetén
 
Vegyünk egy tetszőleges nyílt csúcsot: m
f(m) f(m) d*(m) × d  
     

 


Határozzunk meg ebben a keresőgráfban egy olyan mélységet, amely az ismert adatokból meghatározható!

 m-be vezető legrövidebb mélység alatti mélység
m csúcs felette van a d szintnek
   
legyen r a d-szintnél mélyebben lévő csúcs:
   
d*(r) > d  
f(r) d*(r) × d
ö
  
 
ý
 d*(r) × d > d × d
d*(r) > d
ø
  
   
tehát f(r) > f(m)
   
d szint felett véges sok csúcsunk van. Véges sok f(m) -nél nyílt csúcsunk van.

Nem csak kikerülhetnek nyílt csúcsok, de be is kerülhetnek, DE csak véges sokszor. (Az algoritmus működése során egy csúcs többször is bekerülhet a nyílt csúcsok közé; többször is ki lehet azt választani kiterjesztésre, de csak véges sokszor biztos, hogy minden csúcs véges sok lépés után kikerül a nyílt csúcsok közül.

 

Bizonyítás (2. lemma):

A bizonyítás indukcióval történik.
Első kiterjesztésre kiválasztás előtt van az optimális útnak eleme (a start csúcs). Vegyünk az optimális utak közül egyet:

s =
n1 start csúcs
  n2  
  ...  
t =
nk utolsó csúcs, terminális

Indukciós feltétel: a k. kiterjesztés előtt tegyük fel, hogy ennek az optimális megoldásnak az i. csúcsa eleme a nyílt csúcsok halmazának (ni Nyílt).
A (k+1). kiterjesztés előtt mi a helyzet?

A k. lépésben kiterjesztéskor pont az ni -t terjesztettük ki. Előállítottuk az összes gyermekét, köztük ni+1 -et.
Ha nem szerepelt: felvesszük nyílt csúcsként.
Ha szerepelt (zárt csúcsként): akkor más úton már eljutottunk hozzá. Utódjai közül pár benne van a keresőgráfban pár nyílt csúcsként szerepel.

Ha nem az ni -t választjuk kiterjesztésre: ő ott marad nyíltként.

 

A kettő következménye:

Az A-algoritmus nem garantálja, hogy az optimális megoldással terminál. Ha van megoldás, akkkor megoldással terminál.
Bizonyítása: konstruktív módon:

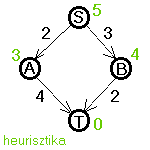
Heurisztika:
S: 5
  
Nyílt:
 
Zárt:
 
A: 3
  
 
 
B: 4
  
S0(0+5)
 
 
T: 0
  
AS(2+3)
BS(3+4)
  
S0(0+5)
     
TA(6+0)
BS(3+4)
  
AS(2+3)
             


teszt: célcsúcs, kész
Holott: a másik út olcsóbb!!!

Bebizonyítottuk, hogy az A-algoritmus nem garantálja az optimális megoldást!

 

b) A*-algoritmus

Kérdés: A-algoritmussal előállítható-e az optimális megoldás? (az előbb a heurisztika rontotta el)

Ha a heurisztikára adunk egy megkötést, akkor "megjavul". ALULRÓL kell becsülni.
Minden csúcsban h(n) h*(n)

Ekkor garancia lehet az optimális megoldás megtalálására.
Ha a heurisztikánk alsó becslésű: A*-algoritmus. A csúcsokbeli heurisztikánk alulról becsüli a hátralévő optimális út költségét.

Állítás: az A*-algoritmus optimális megoldás megtalálását garantálja

Bizonyítás: optimális megoldás: 0 heurisztika triviális
  Így a szélességire is beláttuk az állításunkat.
   
3. lemma: az A*-algoritmus által kiterjesztésre kiválasztott bármely csúcs kiértékelőfüggvénye nem nagyobb (kisebb egyenlő), mint az optimális út tényleges költsége: f(n) f*(s)

Bizonyítás (3. lemma):

1.
 ha nincs megoldás (opt. költség = ), akkor f(n) = f*(n) = ,triviális eset
2.
 ha van megoldás, akkor van optimális megoldás is
s =
n0
ö
  
  n1
÷
  
    n2
ý
 problémmánk egy aktuális megoldása (opt. megoldása)
  ...
÷
  
t =
nk
ø
  
       
Ennek az útnak lesz mindig eleme. Vegyük a legelső olyan elemet, ami a nyílt csúcsok között van: ni. Összes előtte levő: zárt.
       
g(ni) = g*(ni)
         
  n - legyen ez az a csúcs, amelyet kiválasztottunk kiterjesztésre
         
  f(n) f(összes_többi_nyílt_csúcs) ,azaz f(n) f(ni) (például)
         
 
f(n)
f(ni) =
g(ni)
+ h(ni) g*(ni) + h*(ni) = f*(ni) = f*(s)
     
¯
¯
    
     
g*(ni)
     [h(ni) h*(ni)] (az alsó becslés miatt)
         


Vagyis: f(n) f*(s). Ezt akartuk belátni.

Az A*-algoritmus az optimális megoldással terminál, ha van megoldás.

 

c) Monoton A-algoritmus

Az A-algoritmusnál a gond: zárt csúcsok. Ugyanazt a csúcsot esetleg többször is ki kell terjeszteni (zárt csúcsok problémája).
Optimális kereső: speciális A-algoritmus, ahol a heurisztika 0. De van-e nem azonos nulla heurisztikával rendelkező algoritmus, mely ilyen tulajdonsággal bír? (vagyis ahol nem merül fel a zárt csúcsok problémája)

Monoton heurisztika:

h(n) h(m) + k(n,m) "(n,m) E esetben
   
Azaz: szülő heurisztikája gyermek heurisztikája + szülőből gyermekbe jutás költsége.

Az ilyen tulajdonságú A-algoritmus: monoton A-algoritmus.
     
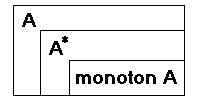  Monoton heurisztikával rendelkezőA-alg. A*-alg. is egyben.
 
 
     



Tétel: Ha h monoton heurisztika, akkor h(n) h*(n)

Bizonyítás:

a)
 ha n-ből nem érhető el egyetlen terminális csúcs sem
  h(n) = h*(n) =
b)
 ha n-ből elérhető valamelyik terminális csúcs
    n0,n1,n2,...,nl = t
     
    h(n0) h(n1) + k(n0,n1)
    h(n1) h(n2) + k(n1,n2)
    ...
    h(nl-1) h(nl) + k(nl-1,nl)
     
   
           
¯
  
           
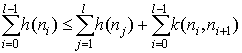h*(n)
 (a hátralévő optimális út költsége)
     
    h(n0) - h(nl) h*(n)   (a többi páronként 0)
     
    h(n) h*(n)   (mivel nl terminális csúcs, így heurisztikája 0)
         

 


A tételt ezzel bebizonyítottuk!

Monoton heurisztika esetén bebizonyítható, hogy tetszőleges kiterjesztésre kiválasztott nyílt csúcs olyan, hogy az adott csúcsban a kiértékelő függvényben olyan értékkel számolunk, ami már optimális.

Tétel: a monoton heurisztikájú A-algoritmus által kiterjesztésre kiválasztott minden nyílt csúcsra igaz, hogy g(n) = g*(n)

Vagyis optimális megoldást állít elő, ill. a zárt csúcsok problémája itt nincs jelen! (hasonlóan mint az optimális keresőknél)

Bizonyítás:

  s = n0,n1,...,nl = n optimális út
         
  n Nyílt és kiterjesztésre n-et választjuk
  Indukciós feltevés: t.f.h. még nem találtuk meg a hozzávezető opt. utat: g(n) > g*(n)
         
  ni az optimális utunk első nyílt csúcsok közötti eleme
         
  f(ni) = g(ni) + h(ni) = g*(ni) + h(ni)    
  g*(ni) + h(ni+1) + k(ni,ni+1) = g*(ni+1) + h(ni+1)  
  g*(ni+1) + h(ni+2) + k(ni+1,ni+2) = g*(ni+2) + h(ni+2)  
  ... g*(nl) + h(nl)  
         
  Hol is tartunk?
         
  f(ni) g*(n) + h(n) < g(n) + h(n) = f(n) ELLENTMONDÁS!
         

 


Tehát a zárt csúcsok problémája a monoton A-algoritmusnál nem lép fel!
(Ha egy csúcs zárt csúcs lett, akkor azzal már nem kell foglalkozni).

  a - súly
     
 
a = 0
 best-first
 
a = 1
 optimális kereső


 

A keresés során változtathatjuk is ezeket a súlyokat, s áttérhetünk az egyikről a másikra. Ilyen pl. a B-algoritmus!

Legyen P és Q két A*-algoritmus. Hasonlítsuk össze a kettőt a heurisztika alapján.

P jobban informált mint Q, ha

hQ(n) < hP(n) h*(n)

Egy jobban informált nem használ nagyobb gráfot mint a kevésbé informált.

Tétel:

Legyen P és Q két A*-algoritmus.
Ha P jobban informált, mint Q Q minden olyan csúcsot kiterjeszt, amit P is.

Bizonyítás:

T.f.h. P kiterjeszt egy n Nyílt csúcsot. Ekkor (lemma 3 segítségével): fP(n) f*(s)
         
 
n' s n :
fP(n') f*(s)
         
 
mivel P jobban informált, mint Q
hQ(n') < hP(n')
         
  fQ(n') = g(n') + hQ(n') < g(n') + hP(n') = fP(n') f*(s)
         

 

2.2.2.2.5. B-algoritmus

Indulunk az A-algoritmussal, de regisztráljuk az addigi legnagyobb kiértékelő függvényű csúcsot.
Addigi Ln := f(s)

Ha a kiértékelőfüggvény az addigi Ln-nál kisebb, akkor opt. keresővel folytatjuk, egyébként meg A*-gal.
Ha h(n) h*(n) ,akkor ugyanazt állítja elő, mint az A*-algoritmus, csak a kiterjesztések száma lecsökken.