alak_A

\(P=\frac{3(\overline{Y}-\rm{Me})}{\sigma}\)

\(\alpha_3=\frac{\frac{\sum_{k=1}^n (Y_k-\overline{Y})^3}{n}}{\sigma^3}\)

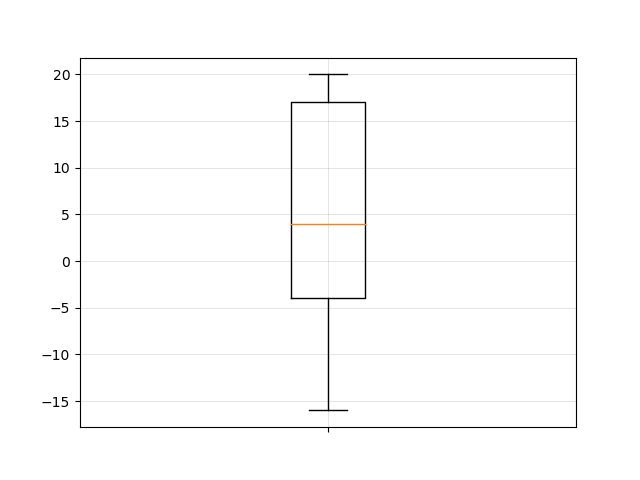
1. feladat

3, -13, 18, 11, 9, 18, -20, 15, 18, -5, 0, 11, 2

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?
P
\(\alpha_3\)

1. eredmények

3, -13, 18, 11, 9, 18, -20, 15, 18, -5, 0, 11, 2

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?	értelmezés
P	-0.9856	balra hosszan elnyúló
\(\alpha_3\)	-0.736	balra hosszan elnyúló

---

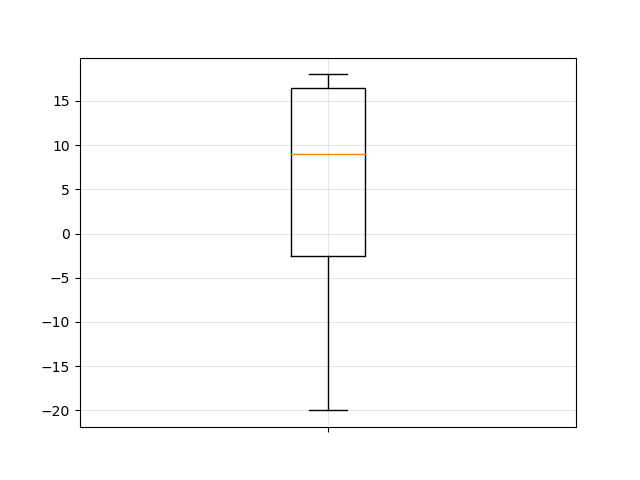
2. feladat

0, -19, 16, 0, -2, 2, -6, 13, -2, -18, 10, 10, -17, -8, -14, 12

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?
P
\(\alpha_3\)

2. eredmények

0, -19, 16, 0, -2, 2, -6, 13, -2, -18, 10, 10, -17, -8, -14, 12

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?	értelmezés
P	-0.1169	balra hosszan elnyúló
\(\alpha_3\)	-0.1021	balra hosszan elnyúló

---

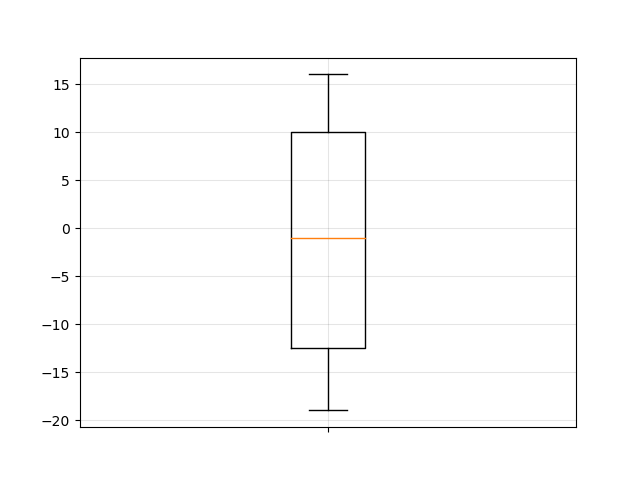
3. feladat

-13, 1, 13, 20, 1, -6, 2, -19, -20, 14, -16, 2, -19, 11, 14

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?
P
\(\alpha_3\)

3. eredmények

-13, 1, 13, 20, 1, -6, 2, -19, -20, 14, -16, 2, -19, 11, 14

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?	értelmezés
P	-0.4506	balra hosszan elnyúló
\(\alpha_3\)	-0.0903	balra hosszan elnyúló

---

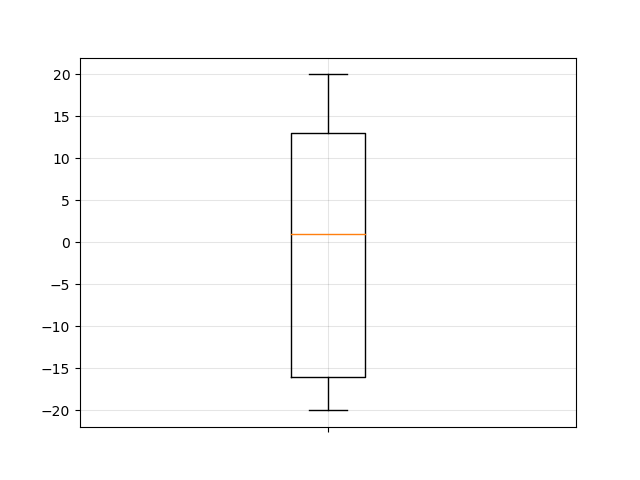
4. feladat

18, 19, -4, 20, -16, 4, 18, 7, 4, 5, 15, -2, -13, -11, 4, 16, -4

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?
P
\(\alpha_3\)

4. eredmények

18, 19, -4, 20, -16, 4, 18, 7, 4, 5, 15, -2, -13, -11, 4, 16, -4

A fenti adatokkal számoljuk ki a hiányzó mennyiségeket:

mi?	mennyi?	értelmezés
P	0.1854	jobbra hosszan elnyúló
\(\alpha_3\)	-0.2442	balra hosszan elnyúló

---