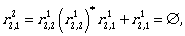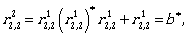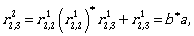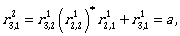Copyright © 2014 Géza Horváth, Benedek Nagy, University of Debrecen
Table of Contents
- Formal Languages and Automata Theory
- Introduction
- 1. Elements of Formal Languages
- 2. Regular Languages and Finite Automata
- 3. Linear Languages
- 4. Context-free Languages
- 5. Context-Sensitive Languages
- 6. Recursively Enumerable Languages and Turing Machines
- 7. Literature
List of Figures
- 2.1. In derivations the rules with long right hand side are replaced by chains of shorter rules, resulting binary derivation trees in the new grammar.
- 2.2. The graph of the automaton of Example 21.
- 2.3. The graph of the automaton of Exercise 19.
- 2.4. The graph of the automaton of Exercise 22.
- 2.5. The graph of the automaton of Exercise 25.
- 2.6. The graph of the automaton of Example 26.
- 2.7. The equivalence of the three types of descriptions (type-3 grammars, regular expressions and finite automata) of the regular languages.
- 2.8. The graph of the automaton of Exercise 31.
- 2.9. The graph of the automaton of Exercise 32.
- 2.10. The graph of the automaton of Exercise 37.
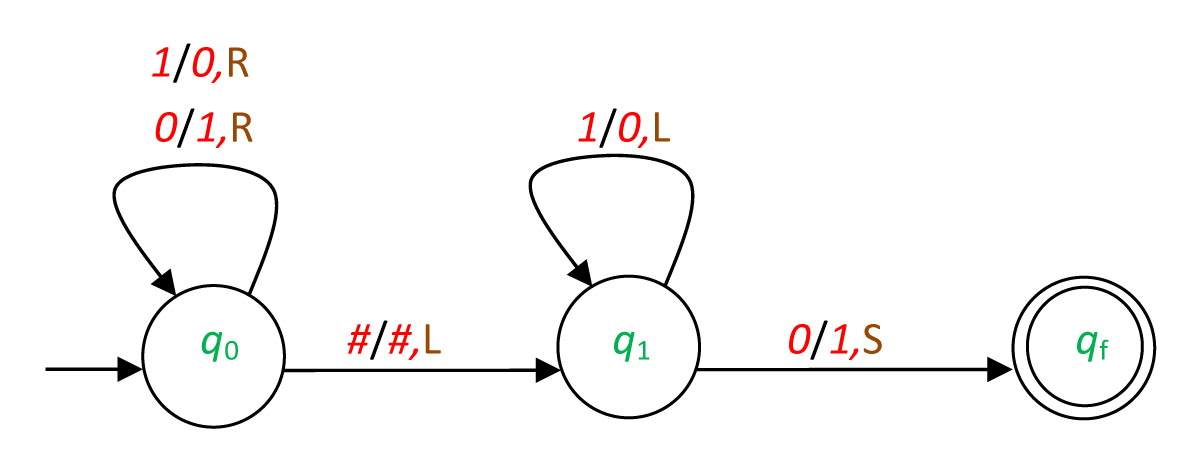
- 2.11. The graph of the Mealy automaton of Example 30.
- 2.12. The graph of the Mealy automaton of Exercise 42.
- 2.13. The graph of the Mealy automaton of Exercise 33.
- 2.14. The graph of the Mealy automaton of Exercise 46.
- 3.1. In derivations the rules with long right hand side (left) are replaced by chains of shorter rules in two steps, causing a binary derivation tree in the resulting grammar (right).
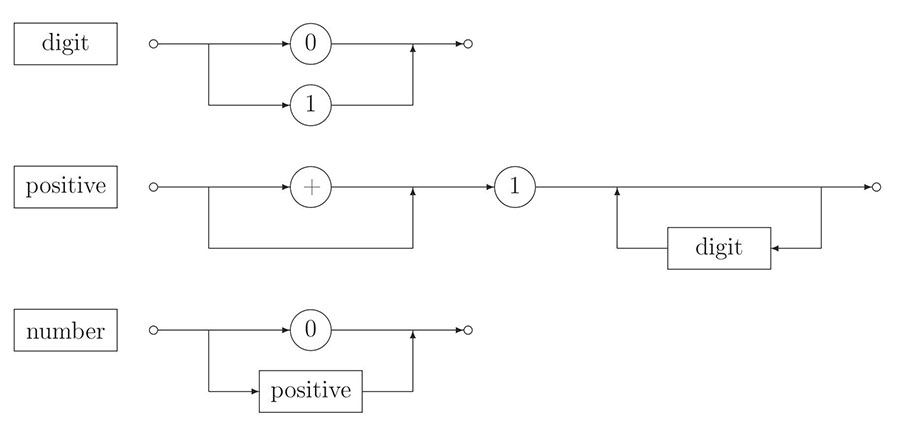
- 4.1. Syntax diagram.
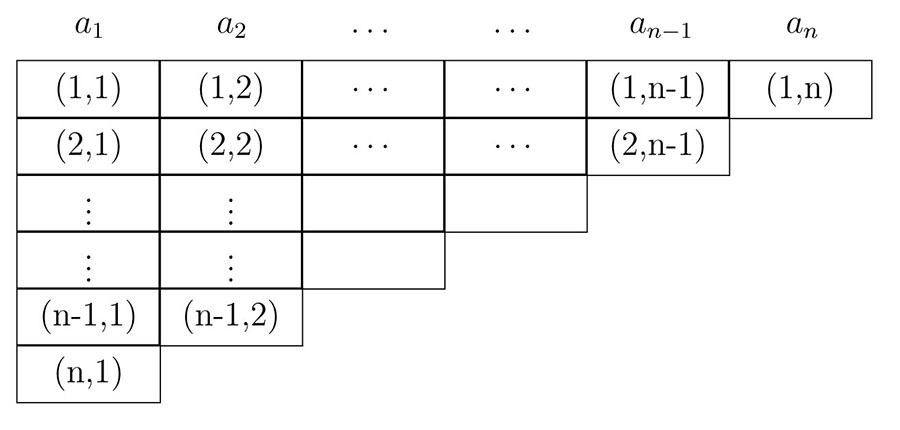
- 4.2. The triangular matrix M for the CYK algorithm.
- 4.3. The triangular matrix M for the CYK algorithm of the Example 45.
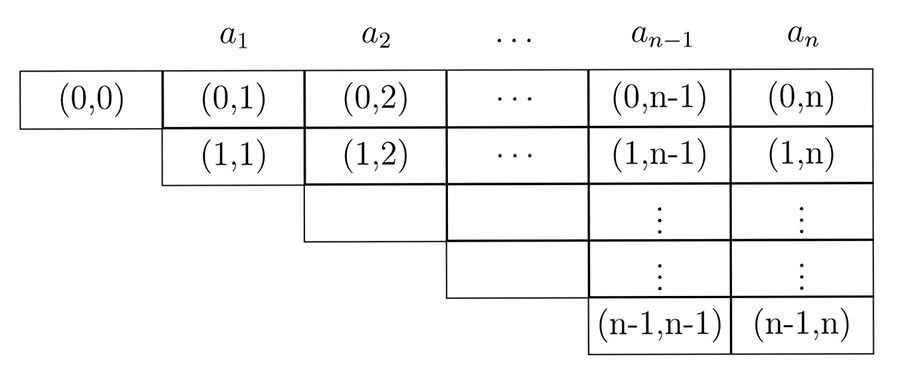
- 4.4. The triangular matrix M for the Earley algorithm.
- 4.5. The triangular matrix M for the Earley algorithm of the example 46.
- 4.6. The graphical notation for the example 47.
- 4.7. The graphical notation for the example 48.
- 4.8. The graphical notation for the example 49.
- 4.9. The graphical notation for the example 50.
- 5.1. In derivations the rules with long right hand side are replaced by chains of shorter rules.
- 6.1. The graphical notation for the Example 58.
List of Tables
Géza Horváth, Benedek Nagy


University of Debrecen, 2014
© Géza Horváth, Benedek Nagy
Typotex Publishing, www.typotex.hu
ISBN: 978-963-279-344-3
Creative Commons NonCommercial-NoDerivs 3.0 (CC BY-NC-ND 3.0) A szerző nevének feltüntetése mellett nem kereskedelmi céllal szabadon másolható, terjeszthető, megjelentethető és előadható, de nem módosítható.
Készült a TÁMOP-4.1.2.A/1-11/1-2011-0063 azonosítószámú „Sokprocesszoros rendszerek a mérnöki gyakorlatban” című projekt keretében.

Formal Languages and Automata Theory are one of the most important base fields of (Theoretical) Computer Science. They are rooted in the middle of the last century, and these theories find important applications in other fields of Computer Science and Information Technology, such as, Compiler Technologies, at Operating Systems, ... Although most of the classical results are from the last century, there are some new developments connected to various fields.
The authors of this book have been teaching Formal Languages and Automata Theory for 20 years. This book gives an introduction to these fields. It contains the most essential parts of these theories with lots of examples and exercises. In the book, after discussing some of the most important basic definitions, we start from the smallest and simplest class of the Chomsky hierarchy. This class, the class of regular languages, is well known and has several applications; it is accepted by the class of finite automata. However there are some important languages that are not regular. Therefore we continue with the classes of linear and context-free languages. These classes have also a wide range of applications, and they are accepted by various families of pushdown automata. Finally, the largest classes of the hierarchy, the families of context-sensitive and recursively enumerable languages are presented. These classes are accepted by various families of Turing machines. At the end of the book we give some further literature for those who want to study these fields more deeply and/or interested to newer developments.
The comments of the lector and some other colleagues are gratefully acknowledged.
Debrecen, 2014.
Géza Horváth and Benedek Nagy
Summary of the chapter: In this chapter, we discuss the basic expressions, notations, definitions and theorems of the scientific field of formal languages and automata theory. In the first part of this chapter, we introduce the alphabet, the word, the language and the operations over them. In the second part, we show general rewriting systems and a way to define algorithms by rewriting systems, namely Markov (normal) algorithms. In the third part, we describe a universal method to define a language by a generative grammar. Finally, in the last part of this chapter we show the Chomsky hierarchy: a classification of generative grammars are based on the form of their production rules, and the classification of formal languages are based on the classification of generative grammars generating them.
An alphabet is a finite nonempty set of symbols. We can use the union, the intersection and the relative complement set operations over the alphabet. The absolute complement operation can be used if a universe set is defined.
Example 1. Let the alphabet E be the English alphabet, the alphabet V contains the vowels,
and the alphabet C is the set of the consonants.
Then V∪C=E, V∩C=∅ and 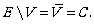
A word is a finite sequence of symbols of the alphabet. The length of the word is the number of symbols it is composed of, with repetitions. Two words are equal if they have the same length and they have the same letter in each position. This might sound trivial, but let us see the following example:
Example 2. Let the alphabet V={1,2,+} and the words p=1+1, q=2. In this case 1+1≠ 2, i.e. p≠q, because these two words have different lengths, and also different letters in the first position.
There is a special operation on words called concatenation, this is the operation of joining two words end to end.
Example 3. Let the alphabet E be the English alphabet. Let the word p=railway, and the word q=station over the alphabet E. Then, the concatenation of p and q is p· q=railwaystation. The length of p is ∣p∣=7 and the length of q is ∣q∣=7, as well.
If there is no danger of confusion we can omit the dot from between the parameters of the concatenation operation. It is obvious that the equation ∣pq∣=∣p∣+∣q∣ holds for all words p and q. There is a special word called an empty word, whose length is 0 and denoted by λ. The empty word is the identity element of the concatenation operation, λp=pλ=p holds for each word p over any alphabet. The word u is a prefix of the word p if there exists a word w such that p=uw, and the word w is a suffix of the word p if there exists a word u such that p=uw. The word v is a subword of word p if there exists words u,w such that p=uvw. The word u is a proper prefix of the word p, if it is a prefix of p, and the following properties hold: u≠λ and u≠p. The word w is a proper suffix of the word p, if it is a suffix of p, and w≠λ, w≠ p. The word v is a proper subword of the word p, if it is a subword of p, and v≠λ, v≠p. As you can see, both the prefixes and suffixes are subwords, and both the proper prefixes and proper suffixes are proper subwords, as well.
Example 4. Let the alphabet E be the English alphabet. Let the word p=railwaystation, and the words u=rail, v=way and w=station. In this example, the word u is a prefix, the word w is a suffix and the word v is a subword of the word p. However, the word uv is also a prefix of the word p, and it is a subword of the word p, as well. The word uvw is a suffix of the word p, but it is not a proper suffix.
We can use the exponentiation operation on a word in a classical way, as well. p0=λ by definition,
p1=p,
and pi=pi-1p,
for each integer i ≥ 2.
The union of pi for each integer i ≥ 0 is denoted by p*,
and the union of pi for each integer i ≥ 1 is denoted
by p+.
 These operations are called Kleene star and Kleene plus operations.
p*=p+∪{λ} holds for each word p,
and if p≠λ
then p+=p* \ {λ}.
We can also use the Kleene star and Kleene plus operations on an alphabet. For an alphabet V we denote the set of all words
over the alphabet by V *, and the set of all words, but the empty word by V +.
These operations are called Kleene star and Kleene plus operations.
p*=p+∪{λ} holds for each word p,
and if p≠λ
then p+=p* \ {λ}.
We can also use the Kleene star and Kleene plus operations on an alphabet. For an alphabet V we denote the set of all words
over the alphabet by V *, and the set of all words, but the empty word by V +.
A language over an alphabet is not necessarily a finite set of words, and it is usually denoted by L.
For a given alphabet V the language L over V is
L ⊆ V *. We have a set again, so we can use the classical
set operations, union, intersection, and the complement operation, if the operands are defined over the same alphabet.
For the absolute complement operation we use V * for universe, so 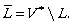 We can also use the concatenation operation. The concatenation of the languages L1 and
L2 contains
all words pq where p ∈ L1 and q ∈
L2. The exponentiation operation is defined in a classical way,
as well. L0={λ} by definition, L1=L,
and Li=Li-1· L,
for each integer i ≥ 2.
The language L 0 contains exactly one word, the empty word. The empty language does not contain any words,
Le=∅, and L 0 ≠ Le.
We can also use the Kleene star and
Kleene plus closure for languages.
We can also use the concatenation operation. The concatenation of the languages L1 and
L2 contains
all words pq where p ∈ L1 and q ∈
L2. The exponentiation operation is defined in a classical way,
as well. L0={λ} by definition, L1=L,
and Li=Li-1· L,
for each integer i ≥ 2.
The language L 0 contains exactly one word, the empty word. The empty language does not contain any words,
Le=∅, and L 0 ≠ Le.
We can also use the Kleene star and
Kleene plus closure for languages.
 so L*=L + if and only if λ ∈ L.
so L*=L + if and only if λ ∈ L.
The algebraic approach to formal languages can be useful for readers who prefer the classical mathematical models. The free monoid on an alphabet V is the monoid whose elements are from V *. From this point of view both operations, concatenation, (also called product) - which is not a commutative operation in this case -, and the union operation (also called addition), create a free monoid on set V, because these operations are associative, and they both have an identity element.
Associative:
(L1 · L2) · L3 = L1 · (L2 · L3),
(L1 ∪ L2) ∪ L3 = L1 ∪ (L2 ∪ L3),
where L1, L2, L3 ⊆ V *.
Identity element:
L0 · L1 = L1 · L0 = L1,
Le ∪ L1 = L1 ∪ Le = L1,
where L1 ⊆ V *, L 0= {λ}, Le = ∅.
The equation Le · L1 = L1 · Le = Le also holds for each L1 ⊆ V *.
In this section, the definition of basic rewriting systems in general and a specific one, the Markov algorithm is presented.
Definition 1. A formal system (or rewriting system) is a pair W = ( V, P ), where V is an alphabet and P is a finite subset of the Cartesian product V *× V *. The elements of P are the (rewriting) rules or productions. If ( p, q ) ∈ P, then we usually write it in the form p → q. Let r, s ∈ V *, and we say that s can be directly derived (or derived in one step) from r (formally: r ⇒ s) if there are words p, p', p'', q ∈ V * such that r = p' pp'', s = p' qp'' and p → q ∈ P. The word s can be derived from r (formally: r ⇒ * s) if there is a sequence of words r0, r1, ..., rk ( k ≥ 1 ) such that r0 = r, rk = s and ri ⇒ ri+1 holds for every 0 ≤ i < k. Moreover, we consider the relation r ⇒* r for every word r ∈ V *. (Actually, the relation ⇒* is the reflexive and transitive closure of the relation ⇒.
A rewriting (or derivation) step can be understood as follows: the word s can be obtained from the word r in such a way that in s the right hand side q of a production of P is written instead of the left hand side p of the same production in r.
Example 5. Let W = ( V, P ) with V = { a, b, c, e, l, n, p, r, t } and P = { able → can, r → c, pp → b }. Then applerat ⇒ applecat ⇒ ablecat ⇒ cancat, and thus applerat ⇒* cancat in the system W.
Now, we are going to present a special version of the rewriting systems that is deterministic, and was given by the Russian mathematician A. A. Markov as normal algorithms.
Definition 2. M = ( V, P, H ) is a Markov (normal) algorithm where
V is a finite alphabet,
P is a finite ordered set (list) of productions of the form V* × V *,
H ⊆ P is the set of halting productions.
The execution of the algorithm on input w ∈ V * is as follows:
Find the first production in P such that its left-hand-side p is a subword of w. Let this production be p → q. If there is no such a production, then step 5 applies.
Find the first (leftmost) occurrence of p in w (such that w = p'pp'' and p'p contains the subword p exactly once: as a suffix).
Replace this occurrence of p in w by the right hand side q of the production.
If p → q ∈ H, i.e., the applied production is a halting production, then the algorithm is terminated with the obtained word (string) as an output.
If there are no productions in P that can be applied (none of their left-hand-side is a subword of w), then the algorithm terminates and w is its output.
If a rewriting step is done with a non halting production, then the algorithm iterates (from step 1) for the newly obtained word as w.
We note here that rules of type λ → q also can be applied to insert word q to the beginning of the current (input) word.
The Markov algorithm may be terminated with an output, or may work forever (infinite loop).
Example 6. Let M = ({1,2,3 },{21→ 12, 31→ 13, 32→ 23},{}) be a Markov algorithm. Then, it is executed to the input 1321 as follows:
1321 ⇒ 1312 ⇒ 1132 ⇒ 1123.
Since there are no more applicable productions, it is terminated. Actually, it is ordering the elements of the input word in a non-decreasing way.
Example 7. Let
W=({a,b,c},{aa → bbb, ac→ bab, bc → a},{}).
Let us apply the algorithm W to the input
ababacbbaacaa.
As it can be seen in Animation 1, the output is
ababbabbbbbabbb.
(For better understanding in the Animation the productions of the algorithm is numbered.)
Exercise 1. Execute the Markov algorithm
M = ({ 1, + }, { 1 + → + 1, + + → +, + → λ } ,{ + → λ })
on the following input words:
1 + 1 + 1 + 1,
11 + 11 + 11,
111,
111 + 1 + 11.
Exercise 2. Execute the Markov algorithm M = ({1,×, a,b },
{ × 11 → a × 1, × 1 → a, 1a → a1b, ba → ab, b1 → 1b, a1 → a, ab → b, b → 1 } ,{ })
on the following input words:
1 × 1,
11 × 11,
111 × 1,
111 × 11.
The previous two exercises are examples for Markov algorithms that compute unary addition and unary multiplication, respectively.
It is important to know that this model of the algorithm is universal in the sense that every problem that can be solved in an algorithmic way can be solved by a Markov algorithm as well.
In the next section, other variations of the rewriting systems are shown: the generative grammars, which are particularly highlighted in this book. As we will see, the generative grammars use their productions in a non-deterministic way.
The generative grammar is a universal method to define languages. It was introduced by Noam Chomsky in the 1950s. The formal definition of the generative grammar is the following:
Definition 3. The generative grammar (G) is the following quadruple:
G = ( N, T, S, P )
where
N is the set of the nonterminal symbols, also called variables, (finite nonempty alphabet),
T is the set of the terminal symbols or constants (finite nonempty alphabet),
S is the start symbol, and
P is the set of the production rules.
The following properties hold: N ∩ T = ∅ and S ∈ N.
Let us denote the union of the sets N and T by V ( V = N ∪ T). Then, the form of the production rules is V *N V * → V *.
Informally, we have two disjoint alphabets, the first alphabet contains the so called start symbol, and we also have a set of productions. The productions have two sides, both sides are words over the joint alphabet, and the word on the left hand side must contain a nonterminal symbol. We have a special notation for the production rules. Let the word p be the left hand side of the rule, and the word q be the right hand side of the rule, then we use the p → q ∈ P expression.
Example 8. Let the generative grammar G be G = ( N, T, S, P ), where
N = {S,A}, T = {a,b}, and P = { S → bAbS, bAb → bSab, A → λ, S → aa }.
In order to understand the operation of the generative grammar, we have to describe how we use the production rules to generate words. First of all, we should give the definition of the derivation.
Definition 4. Let G = ( N, T, S, P ) be a generative grammar, and let p and q be words over the joint alphabet V = N ∪ T. We say that the word q can be derived in one step from the word p, if p can be written in a form p = uxw, q can be written in a form q = uyw, and x → y ∈ P. (Denoted by p ⇒ q.) The word q can be derived from the word p, if q = p or there are words r1, r2,..., rn such that r1 = p, rn = q and the word ri can be derived in one step from the word ri-1, for each 2 ≤ i ≤ n. (Denoted by p ⇒* q.)
Now, that we have a formal definition of the derivation, let us see an example for deeper understanding.
Example 9. Let the generative grammar G be G = ( N, T, S, P ) , where
N = {S,A}, T = {0,1}, and P = { S → 1, S → 1A, A → AA, A → 0, A → 1 }.
Let the words p,t and q be p = A0S0, t = A01A0, and q = A0110. In this example, the word t can be derived from the word p in one step, (p → t), because p can be written in a form p = uxw, where u = A0, x = S, w = 0, and the word t can be written in a form t = uyw, where y = 1A, and S → 1A ∈ P.
The word q can be derived from the word p, (p ⇒*q), because there exist words r1,r2 and r3 such that r1 = p, r2 = t, r3 = q and r1 ⇒ r2 and r2 ⇒ r3.
Now we have all the definitions to demonstrate how we can use the generative grammar to generate a language.
Definition 5. Let G = ( N, T, S, P ) be a generative grammar. The language generated by the grammar G is
L(G)={p∣p ∈ T*, S ⇒* p}.
The above definition claims that the language generated by the grammar G contains each word over the terminal alphabet which can be derived from the start symbol S.
Example 10. Let the generative grammar G be G = ( N, T, S, P ), where
N = {S,A}, T = {a,b}, and P = { S → bb, S → ASA, A → a }.
In this example, the word bb can be derived from the start symbol S in one step, because S → bb ∈ P, so the word bb is in the generated language, bb ∈ L(G).
The word abba can be derived from the start symbol, because S ⇒ ASA, ASA ⇒ aSA, aSA ⇒ abbA, abbA → abba, so the word abba is also in the generated language, abba ∈ L(G).
The word bab can not be derived from the start symbol, so it is not in the generated language, bab ∉ L(G).
In this case, it is easy to determine the generated language, L(G) = {aibbai∣i ≥ 0}.
Exercise 3. Create a generative grammar G, which generates the language L = {a*b+c*}!
Exercise 4. Create a generative grammar G, which generates the language of all binary numbers!
The Chomsky hierarchy was described first by Noam Chomsky in 1956. It classifies the generative grammars based on the forms of their production rules. The Chomsky hierarchy also classifies languages, based on the classes of generative grammars generating them. The formal definition is provided below.
Definition 6. (Chomsky hierarchy) Let G = ( N, T, S, P ) be a generative grammar.
Type 0 or unrestricted grammars. Each generative grammar is unrestricted.
Type 1 or context-sensitive grammars. G is called context-sensitive, if all of its production rules have a form
p1Ap2 → p1qp2,
or
S → λ,
where p1, p2 ∈ V *, A ∈ N and q ∈ V +. If S → λ ∈ P then S does not appear in the right hand side word of any other rule.
Type 2 or context-free grammars. The grammar G is called context-free, if all of its productions have a form
A → p,
where A ∈ N and p ∈ V *.
Type 3 or regular grammars. G is called regular, if all of its productions have a form
A → r,
or
A → rB,
where A,B ∈ N and r ∈ T *.
Example 11. Let the generative grammar G0 be
G0 = ({S,X},{x,y},S,P) P = { S → SXSy, XS → y, X → SXS, S → yxx }.
This grammar is unrestricted, because the second rule is not a context-sensitive rule.
Example 12. Let the generative grammar G1 be
G1 = ({S,X},{x,y},S,P) P = { S → SXSy, XSy → XyxXy, S → yXy, X → y }.
This grammar is context-sensitive, because each production rule has an appropriate form.
Example 13. Let the generative grammar G2 be
G2 = ({S,X},{x,y},S,P) P = { S → SyS, S → XX, S → yxy, X → ySy, X → λ }.
This grammar is context-free, because the left hand side of each production rule is a nonterminal symbol.
Example 14. Let the generative grammar G be
G = ({S,X},{x,y},S,P) P = { S → xyS, S → X, X → yxS, S → x, X → λ }.
This grammar is regular, because the left hand side of each production rule is a nonterminal, and the right hand side contains at most one nonterminal symbol, in last position.
Exercise 5. What is the type of the following grammars?
1. G = ({S,A},{0,1},S,P) P = { S → 0101A, S → λ, A → 1S, A → 000 }. 2. G = ({S,A,B},{0,1},S,P) P = { S → 0A01B, S → λ, 0A01 → 01A101, A → 0BB1, B → 1A1B, B → 0011, A → 1 }. 3. G = ({S,A,B},{0,1},S,P) P = { S → 0ABS1, S → 10, 0AB → 01SAB, 1SA → 111, A → 0, B → 1 }. 4. G = ({S,A},{0,1},S,P) P = { S → 00A, S → λ, A → λ, A → S1S }.
Definition 7. The language L is regular, if there exists a regular grammar G such that L = L (G).
The same kind of definitions are given for the context-free, context-sensitive, and recursively enumerable languages:
Definition 8. The language L is context-free, if there exists a context-free grammar G such that L = L (G).
Definition 9. The language L is context-sensitive, if there exists a context-sensitive grammar G such that L = L (G).
Definition 10. The language L is called recursively enumerable, if there exists an unrestricted grammar G such that L = L (G).
Although these are the most often described classes of the Chomsky hierarchy, there are also a number of subclasses which are worth investigating. For example, in chapter 3 we introduce the linear languages. A grammar is linear, if it is context-free, and the right hand side of its rules contain maximum one nonterminal symbol. The class of linear languages is a proper subset of the class of context-free languages, and it is a proper superset of the regular language class. Example 15. shows a typical linear language and a typical linear grammar.
Example 15. Let L be the language of the palindromes over the alphabet T = {a,b}. (Palindromes are words that read the same backward or forward.) Language L is generated by the following linear grammar.
G = ({S},{a,b},S,P) P = { S → aSa, S → bSb, S → a, S → b, S → λ }.
Language L is linear, because it can be generated by the linear grammar G.
Example 16. In Example 9 we can see a context-free grammar, which is not linear, because the production A → AA is not a linear rule. However, this context-free grammar generates a regular language, because the same language can be generated by the following regular grammar.
G = ({S,A},{0,1},S,P, and P = { S → 1A, A → 1A, A → 0A, A → λ }.
It is obvious that context-sensitive grammars are unrestricted as well, because each generative grammar is unrestricted. It is also obvious that regular grammars are context-free as well, because in regular grammars the left hand side of each rule is a nonterminal, which is the only condition to be satisfied for a grammar in order to be context-free.
Let us investigate the case of the context-free and context sensitive grammars.
Example 17. Let the grammar G be
G = ({S,A},{x,y},S,P) P = { S → AxA, A → SyS, A → λ, S → λ }.
This grammar is context-free, because the left hand side of each rule contains one nonterminal. At the same time, this grammar is not context-sensitive, because
the rule A → λ is not allowed in context-sensitive grammars,
if S → λ ∈ P, then the rule A → SyS is not allowed.
This example shows that there are context-free grammars which are not context-sensitive. Although this statement holds for grammars, we can show that in the case of languages the Chomsky hierarchy is a real hierarchy, because each context-free language is context-sensitive as well. To prove this statement, let us consider the following theorem.
Theorem 1. For each context-free grammar G we can give context-free grammar G', which is context-sensitive as well, such that L (G) = L (G').
Proof. We give a constructive proof of this theorem. We are going to show the necessary steps to receive an equivalent context-sensitive grammar G' for a context-free grammar G = ( N, T, S, P ).
First, we have to collect each nonterminal symbol from which the empty word can be derived. To do this, let the set U (1) be U (1) = {A∣A ∈ N, A → λ ∈ P}. Then let U (i) = U (i-1) ∪ {A∣A → B1B2...Bn ∈ P, B1, B2,..., Bn ∈ U (i-1)}. Finally, we have an integer i such that U (i) = U (i-1) = U which contains all of the nonterminal symbols from which the empty word can be derived.
Second, we are going to create a new set of rules. The right hand side of these rules should not contain the empty word. Let P' = (P ∪ P1)\{A→ λ∣A ∈ N}. The set P1 contains production rules as well. B → p ∈ P1 if B → q ∈ P and we get p from q by removing some letters contained in set U.
Finally, if S ∉ U, then G' = ( N, T, S, P' ). If set U contains the start symbol, then the empty word can be derived from S, and λ∈ L (G). In this case, we have to add a new start symbol to the set of nonterminals, and we also have to add two new productions to the set P1, and G' = ( N ∪{S'}, T, S', P' ∪ {S' → λ, S' → S}), so G' generates the empty word, and it is context sensitive.
QED.
Example 18. Let the context-free grammar G be
G = ({S,A,B},{x,y},S,P) P = { S → ASxB, S → AA, A → λ, B → SyA }.
Now, we create a context-sensitive generative grammar G', such that L (G') = L (G).
1. U (1) = {A}, U (2) = {A,S} = U. 2. P' = { S → ASxB, S → SxB, S → AxB, S → xB, S → AA, S → A, B → SyA, B → yA, B → Sy, B → y }. 3. G' = ({S,A,B,S'},{x,y},S',P' ∪{S' → λ, S' → S}).
Exercise 6. Create a context-sensitive generative grammar G', such that L (G') = L (G)!
G = ({S,A,B,C},{a,b},S,P) P = { S → aAbB, S → aCCb, C → λ, A → C, B → ACC, A → aSb }.
Exercise 7. Create a context-sensitive generative grammar G', such that L (G') = L (G)!
G = ({S,X,Y},{0,1},S,P) P = { S → λ, S → XXY, X → Y0Y1, Y → 1XS1, X → S00S }.
In the following chapters we are going to investigate the language classes of the Chomsky hierarchy. We will show algorithms to decide if a word is in a language generated by a generative grammar. We will learn methods which help to specify the position of a language in the Chomsky hierarchy, and we are going to investigate the closure properties of the different language classes.
We will introduce numerous kinds of automata. Some of them accept languages, and we can use them as an alternative language definition tool, however, some of them calculate output words from the input word, and we can see them as programmable computational tools. First of all, in the next chapter, we are going to deal with the most simple class of the Chomsky hierarchy, the class of regular languages.
Table of Contents
Summary of the chapter: In this chapter, we deal with the simplest languages of the Chomsky hierarchy, i.e., the regular languages. We show that they can be characterized by regular expressions. Another description of this class of languages can be given by finite automata: both the class of deterministic finite automata and the class of nondeterministic finite automata accept this class. The word problem (parsing) can be solved in real-time for this class by the deterministic finite automata. This class is closed under regular and under set-theoretical operations. This class also has a characterization in terms of analyzing the classes of possible continuations of the words (Myhill-Nerode theorem). We also present Mealy-type and Moore-type transducers: finite transducers are finite automata with output.
In order to be comprehensive we present the definition of regular grammars here again.
Definition (Regular grammars). A grammar G=(N,T,S,P) is regular if each of its productions has one of the following forms: A → u, A → uB, where A,B∈ N, u∈ T*. The languages that can be generated by regular grammars are the regular languages (they are also called type 3 languages of the Chomsky hierarchy).
Animation 2. presents an example for a derivation in a regular grammar.
We note here that the grammars and languages of the definition above are commonly referred to as right-linear grammars and languages, and regular grammars and languages are defined in a more restricted way:
Definition 12. (Alternative definition of regular grammars). A grammar G = ( N, T, S, P ) is regular if each of its productions has one of the following forms: A → a, A → aB, S → λ, where A,B ∈ N, a ∈ T. The languages that can be generated by these grammars are the regular languages.
Now we show that the two definitions are equivalent in the sense that they define the same class of languages.
Theorem 2. The language classes defined by our original definition and by the alternative definition coincide.
Proof. The proof consists of two parts: we need to show that languages generated by grammars of one definition can also be generated by grammars of the other definition.
It is clear the grammars satisfying the alternative definition satisfy our original definition at the same time, therefore, every language that can be generated by the grammars of the alternative definition can also be generated by grammars of the original definition.
Let us consider the other direction. Let a grammar G = ( N, T, S, P ) may contain rules of types A → u and A → uB (A,B ∈ N, u ∈ T*). Then, we give a grammar G' = ( N', T, S', P' ) such that it may only contain rules of the forms A → a, A → aB, S' → λ (where A,B ∈ N', a ∈ T) and it generates the same language as G, i.e., L (G) = L (G').
First we obtain a grammar G'' such that L (G) = L (G'') and G'' = ( N'', T, S, P'' ) may contain only rules of the following forms: A → a, A → aB, A → B, A → λ (where A,B ∈ N'', a ∈ T). Let us check every rule in P: if it has one of the forms above, then we copy it to the set P'', else we will do the following:
if the rule is of the form A → a1... ak for k > 1, where ai ∈ T, i ∈{1,...,k}, then let the new nonterminals X1,..., Xk-1 be introduced (new set for every rule) and added to the set N'' and instead of the actual rule the next set of rules is added to P'': A → a1X1, X1 → a2X2, ..., Xk-2 → ak-1Xk-1, Xk-1 → ak.
if the rule is of the form A → a1... akB for k > 1, where ai ∈ T, i ∈ {1,...,k}, then let the new nonterminals X1,..., Xk-1 be introduced (new set for every rule) and put to the set N'', and instead of the actual rule the next set of rules is added to P'': A → a1X1, X1 → a2X2, ..., Xk-2 → ak-1Xk-1, Xk-1 → akB.
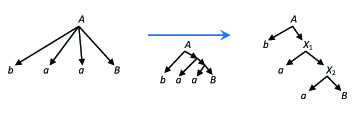
When every rule is analyzed (and possibly replaced by a set of rules) we have grammar G''. It is clear that the set of productions P'' of G'' may contain only rules of the forms A → a, A → aB, A → a, A → λ (where A,B ∈ N'', a∈ T), since we have copied only rules from P that have these forms, and all the rules that are added to the set of productions P'' by replacing a rule are of the forms A → aB, A → a (where A,B ∈ N'', a ∈ T). Moreover, exactly the same words can be derived in G'' and in G. The derivation graphs in the two grammars can be mapped in a bijective way. When a derivation step is applied in G with a rule A → a1... that is not in P'', then the rules must be used in G'' that are used to replace the rule A → a1...: applying the first added rule first A → a1X1, then there is only one rule that can be applied in G'', since there is only one rule added with X1 in its left hand side... therefore, one needs to apply all the rules of the chain that was used to replace the original rule A → a1.... Then, if there is a nonterminal B at the end of the rule A → a1..., then it is located at the end of the last applied rule of the chain, and thus the derivation can be continued in the same way in both grammars. The other way around, if we use a newly introduced rule in the derivation in G'', then we must use all the rules of the chain, and also we can use the original rule that was replaced by this chain of rules in the grammar G. In this way, there is a one-to-one correspondence in the completed derivations of the two grammars. (See Figure 2.1. for an example of replacing a long rule by a sequence of shorter rules.)
Figure 2.1. In derivations the rules with long right hand side are replaced by chains of shorter rules, resulting binary derivation trees in the new grammar.
 |
Now we may have some rules in P'' that do not satisfy the alternative definition. The form of these rules can only be A → B and C → λ (where A,B,C ∈ N'', C ≠ S). The latter types of rules can be eliminated by the Empty-word lemma (see Theorem 1.). Therefore, we can assume that we have a grammar G''' = ( N''', T, S', P''' ) such that L (G''') = L (G) and P''' may contain only rules of the forms A → aB, A → B, A → a, S' → λ (where A,B ∈ N''', a∈ T and in case S' → λ ∈ P''' the start symbol S' does not occur on the right hand side of any of the rules of P'''). Let us define the following sets of nonterminals:
let U1 (A) = {A},
let Ui+1 (A) = Ui (A) ∪ {B ∈ N'''∣∃ C ∈ Ui (A) such that C → B ∈ P'''}, for i > 1.
Since N''' is finite there is a minimal index k such that Uk(A) = Uk+1(A). Let U(A) denote the set Uk(A) with the above property. In this way, U(A) contains exactly those nonterminals that can be derived from A by using rules only of the form B → C (where B,C ∈ N'''). We need to replace the parts A ⇒* B → r of the derivations in G''' by a direct derivation step in our new grammar, therefore, let G' = ( N''', T, S', P' ), where P' = {A → r∣∃ B ∈ N''' such that B → r ∈ P''', r ∉ N''' and B ∈ U(A)}. Then G' fulfills the alternative definition, moreover, it generates the same language as G''' and G.
QED.
Further we will call a grammar a regular grammar in normal form if it satisfies our alternative definitions. In these grammars the structures of the rules are more restricted: if we do not derive the empty word, then we can use only rules that have exactly one terminal in their right hand side.
Example 19. Let
G = ({S,A,B},{0,1,2},S,
{ S → 010B,
A → B,
A → 2021,
B → 2A,
B → S,
B → λ
}). Give a grammar that is equivalent to G and is in normal form.
Solution:
Let us exclude first the rules that contain more than one terminal symbols. Such rules are S → 010B and A → 2021. Let us substitute them by the sets
{S → 0X1, X1 → 1X2, X2 → 0B}
and
{A → 2X3, X3 → 0X4, X4 → 2X5, X5 → 1}
of rules, respectively, where the newly introduced nonterminals are {X1, X2} and {X3, X4, X5}, respectively. The obtained grammar is
G'' = ({S, A, B, X1, X2, X3, X4, X5},{0,1,2},S,
{ S → 0X1,
X1 → 1X2,
X2 → 0B,
A → B,
A → 2X3,
X3 → 0X4,
X4 → 2X5,
X5 → 1,
B → 2A,
B → S,
B → λ
).Now, by applying the Empty-word lemma, we can exclude rule B → λ (the empty word can be derived from the nonterminals B and A in our example) and by doing so we obtain grammar
G''' = ({S, A, B, X1, X2, X3, X4, X5}, {0,1,2}, S,
{ S → 0X1,
X1 → 1X2,
X2 → 0B,
X2 → 0,
A → B,
A → 2X3,
X3 → 0X4,
X4 → 2X5,
X5 → 1,
B → 2A,
B → 2,
B → S
}).Now we are excluding the chain rules A → B, B → S. To do this step, first, we obtain the following sets:
| U0 (S) = {S} | U0 (A) = {A} | U0 (B) = {B} | ||
| U1 (S) = {S} = U(S) | U1 (A) = {A,B} | U1 (B) = {B,S} | ||
| U2 (A) = {A,B,S} | U2 (B) = {B,S} = U(B) | |||
| U3 (A) = {A,B,S} = U(A) |
Actually for those nonterminals that are not appearing in chain rules these sets are the trivial sets, e.g., U (X1) = U0 (X1) = {X1}. Thus, finally, we obtain grammar
G' = ({S, A, B, X1, X2, X3, X4, X5}, {0,1,2}, S,
{ S → 0X1,
A → 0X1,
B → 0X1,
X1 → 1X2,
X2 → 0B,
X2 → 0,
A → 2X3,
X3 → 0X4,
X4 → 2X5,
X5 → 1,
B → 2A,
A → 2A,
B → 2,
A → 2
}).Since our transformations preserve the generated language, every obtained grammar (G'', G''' and also G') is equivalent to G. Moreover, G' is in normal form. Thus the problem is solved.
Exercise 8. Let
G = ({S, A, B, C},{a,b},S,
{ S → abA,
S → A,
A → B,
B → abab,
B → aA,
B → aaC,
B → λ,
C → aaS
}). Give a grammar that is equivalent to G and is in normal form.
Exercise 9. Let
G = ({S, A, B, C},{a,b,c},S,
{ S → A,
S → B,
A → aaB,
B → A,
B → acS,
B → C,
C → c,
C → λ
}). Give a grammar that is equivalent to G and is in normal form.
Exercise 10. Let
G = ({S, A, B, C, D},{a,b,c},S,
{ S → aA,
S → bB,
A → B,
B → A,
B → ccccC,
B → acbcB,
C → caacA,
C → cba
}). Give a grammar that is equivalent to G and is in normal form.
Exercise 11. Let
G = ({S, A, B, C, D},{1,2,3,4},S,
{ S → 11A,
S → 12B,
A → B,
B → C,
B → 14,
B → 4431,
C → 3D,
D → 233C
}). Give a grammar that is equivalent to G and is in normal form.
In this section, we will describe the regular languages in another way. First, we define the syntax and the semantics of regular expressions, and then we show that they describe the same class of languages as the class that can be generated by regular grammars.
Definition 13. (Regular expressions). Let T be an alphabet and V = T ∪ {∅, λ, +, ·, *,(,)} be defined as its extension, such that T ∩ {∅, λ, +, ·, *,(,)} = ∅. Then, we define the regular expressions over T as expressions over the alphabet V in an inductive way:
Base of the induction:
∅ is a (basic) regular expression,
λ is a (basic) regular expression,
every a ∈ T is a (basic) regular expression;
Induction steps
if p and r are regular expressions, then (p+r) is also a regular expression,
if p and r are regular expressions, then (p · r) is also a regular expression (we usually eliminate the sign · and write (pr) instead (p · r)),
if r is a regular expression, then r* is also a regular expression.
Further, every regular expression can be obtained from the basic regular expressions using finite number of induction steps.
Definition 14 (Languages described by regular expressions). Let T be an alphabet. Then, we define languages described by the regular expressions over the alphabet T following their inductive definition.
Basic languages:
∅ refers to the empty language {},
λ refers to the language {λ},
for every a ∈ T, the expression refers to the language {a};
Induction steps:
if p and r refer to the languages Lp and Lr, respectively, then the regular expressions (p+r) refers to the language Lp ∪ Lr,
if p and r refer to the languages Lp and Lr, respectively, then the regular expressions (p · r) or (pr) refers to the language Lp · Lr,
if r refers to a language Lr then r* refers to the language Lr*.
The language operations used in the above definition are the regular operations:
the addition (+) is the union of two languages,
the product is the concatenation of two languages, and
the reflexive and transitive closure of concatenation is the (Kleene-star) iteration of languages.
Two regular expressions are equivalent if they describe the same language. Here are some examples:
| (p+r) | ≡ | (r+p) | (commutativity of union) |
| ((p+r)+q) | ≡ | (p+(r+q)) | (associativity of union) |
| (r+∅) | ≡ | r | (additive zero element, unit element for union) |
| ((pr)q) | ≡ | (p(rq) | (associativity of concatenation) |
| (rλ) | ≡ | (λr) ≡ r | (unit element for concatenation) |
| ((p+r)q) | ≡ | ((pq)+(rq)) | (left distributivity) |
| (p(r+q)) | ≡ | ((pr)+(pq)) | (right distributivity) |
| (r∅) | ≡ | ∅ | (zero element for concatenation) |
| λ * | ≡ | λ | (iteration of the unit element) |
| ∅ * | ≡ | λ | (iteration of the zero element) |
| (rr*) | ≡ | (r*r) | (positive iteration) |
Actually, the values of the last equivalence are frequently used, and they are denoted by r+, i.e., r+ ≡ rr* by definition. This type of iteration which does not allow for 0 times iteration, i.e., only positive numbers of iterations are allowed, is usually called Kleene-plus iteration.
With the use of the above equivalences we can write most of the regular expressions in a shorter form: some of the brackets can be eliminated without causing any ambiguity in the language described. The elimination of the brackets is usually based on the associativity (both for the union and for the concatenation). Some further brackets can be eliminated by fixing a precedence order among the regular operations: the unary operation (Kleene-)star is the strongest, then the concatenation (the product), and (as usual) the union (the addition) is the weakest.
We have regular grammars to generate languages and regular expressions to describe languages, but these concepts are not independent. First we will prove one direction of the equivalence between them.
Theorem 3. Every language described by a regular expression can be generated by a regular grammar.
Proof. The proof goes by induction based on the definition of regular expressions. Let r be a basic regular expression, then
if r is ∅, then the empty language can be generated by the regular grammar
(S, A, T, S, {A → a});
if r is λ, then the language {λ} can be generated by the regular grammar
(S, T, S, {S → λ});
if r is a for a terminal a ∈ T, then the language {a} is generated by the regular grammar
(S, T, S, {S → a}).
If r is not a basic regular expression then the following cases may occur:
r is (p+q) with some regular expressions p,q such that the regular grammars Gp = (Np, T, Sp, Pp) and Gq = (Nq, T, Sq, Pq) generate the languages described by expression p and q, respectively, where Np ∩ Nq = ∅ (this can be done by renaming nonterminals of a grammar without affecting the generated language). Then let
G = (Np ∪ Nq ∪ {S}, T, S, Pp ∪ Pq ∪ {S → Sp, S→ Sq}),
where S ∉ Np ∪ Nq is a new symbol. It can be seen that G generates the language described by expression r.
r is (p · q) with some regular expressions p,q such that the regular grammars Gp = (Np, T, Sp, Pp) and Gq = (Nq, T, Sq, Pq) generate the languages described by expression p and q, respectively, where Np ∩ Nq = ∅. Then let
G = (Np ∪ Nq,T, Sp, Pq ∪ {A → uB∣A → uB ∈ Pp, A,B ∈ Np, u ∈ T*} ∪ {A → uSq∣A → u ∈ Pp, A ∈ Np, u ∈ T*}).
It can be shown that G generates the language described by expression r.
r is a regular expression of the form q* for a regular expression q. Further let Gq = (Nq, T, Sq, Pq) be a regular grammar that generates the language described by expression q. Then, let
G = (Nq ∪ {S},T,S, Pq ∪ {S → λ, S → Sq} ∪ {A → uSq∣A → u ∈ Pq, A ∈ Nq, u ∈ T*}),
where S ∉ Nq. It can be shown that G generates the language described by expression r.
Since every regular expression built by finitely many applications of the induction step, for any regular expression one can construct a regular grammar such that the grammar generates the language described by the expression.
QED.
When we want to have a grammar that generates the language given by a regular expression, the process can be faster, if we know that every singleton, i.e., language containing only one word, can easily be obtained by a grammar having only one nonterminal (the start symbol) and only one production that allows to generate the given word in one step.
Example 20. Let r = (cbb)*(ab+ba) be a regular expression (that describes a language over the alphabet {a,b,c}). Give a regular grammar that generates this language.
Solution:
Let us build up r from its subexpressions. According to the above observation, the language {cbb} can be generated by the grammar
Gcbb =({Scbb},{a,b,c},Scbb,{Scbb → cbb}).
Now, let us use our induction step to obtain the grammar G(cbb)* that generates the language (cbb)*: then
G(cbb)* = ({Scbb, S(cbb)*},{a,b,c},S(cbb)*,
{Scbb → ccb, S(cbb)* → λ, S(cbb)* → Scbb, S(cbb) → cbb S(cbb)}).
The languages {ab} and {ba} can be generated by grammars
Gab = ({Sab},{a,b,c},Sab,{Sab → ab})
and
Gab = ({Sba},{a,b,c},Sba,{Sba → ba}),
respectively. Their union, ab+ba, then is generated by the grammar
Gab+ba = ({Sab,Sba,Sab+ba},{a,b,c},Sab+ba,
{Sab → ab, Sba → ba, Sab+ba → Sab, Sab+ba → Sba})
according to our induction step.
Finally, we need the concatenation of the previous expressions (cbb)* and (ab+ba), and it is generated by the grammar
G(cbb*)(ab+ba) = ({Scbb, S(cbb)*,Sab,Sba,Sab+ba}, {a,b,c}, S(cbb)*,
{Scbb → cbbSab+ba, S(cbb)* → Sab+ba, S(cbb)* → Scbb, S(cbb)* → cbb S(cbb)*,
Sab → ab, Sba → ba, Sab+ba → Sab, Sab+ba → Sba})
due to our induction step. The problem is solved.
Exercise 12. Give a regular expression that describes the language containing exactly those words that contain three consecutive a's over the alphabet {a,b}.
Exercise 13. Give a regular expression that describes the language containing exactly those words that do not contain two consecutive a's (over the alphabet {a,b}).
Exercise 14. Give a regular grammar that generates the language 0*(1+22)(2*+00).
Exercise 15. Give a regular grammar that generates the language 0+1(1+0)*.
Exercise 16. Give a regular grammar that generates the language (a+bb(b+(cc)*))*(ababa+c*).
In this section we first define several variations of the finite automata distinguished by the properties of the transition function.
Definition 15 (Finite automata). Let A = ( Q, T, q0, δ, F ). It is a finite automaton (recognizer), where Q is the finite set of (inner) states, T is the input (or tape) alphabet, q0 ∈ Q is the initial state, F ⊆ Q is the set of final (or accepting) states and δ is the transition function as follows.
δ : Q × (T ∪ {λ}) → 2Q (for nondeterministic finite automata with allowed λ-transitions);
δ : Q × T → 2Q (for nondeterministic finite automata without λ-transitions);
δ : Q × T → Q (for deterministic finite automata, d can be partially defined);
δ : Q × T → Q (for completely defined deterministic finite automata (it is not allowed that δ is partial function, it must be completely defined).
One can observe, that the second variation is a special case of the first one (not having λ-transitions). The third variation is a special case of the second one having sets with at most one element as images of the transition function, while the fourth case is more specific allowing sets exactly with one element.
One can imagine a finite automaton as a machine equipped with an input tape. The machine works on a discrete time scale. At every point of time the machine is in one of its states, then it reads the next letter on the tape (the letter under the reading head), or maybe nothing (in the first variations), and then, according to the transition function (depending on the actual state and the letter being read, if any) it goes to a/the next state. It may happen in some variations that there is no transition defined for the actual state and letter, then the machine gets stuck and cannot continue its run.
There are two widely used ways to present automata: by Cayley tables or by graphs. When an automaton is given by a Cayley table, then the 0th line and the 0th column of the table are reserved for the states and for the alphabet, respectively (and it is marked in the 0th element of the 0th row). In some cases it is more convenient to put the states in the 0th row, while in some cases it is a better choice to put the alphabet there. We will look at both possibilities. The initial state should be the first among the states (it is advisable to mark it by a → sign also). The final states should also be marked, they should be circled. The transition function is written into the table: the elements of the set δ(q,a) are written (if any) in the field of the column and row marked by the state q and by the letter a. In the case when λ-transitions are also allowed, then the 0th row or the column (that contains the symbols of the alphabet) should be extended by the empty word (λ) also. Then λ-transitions can also be indicated in the table.
Automata can also be defined in a graphical way: let the vertices (nodes, that are drawn as circles in this case) of a graph represent the states of the automaton (we may write the names of the states into the circles). The initial state is marked by an arrow going to it not from a node. The accepting states are marked by double circles. The labeled arcs (edges) of the graph represent the transitions of the automaton. If p ∈ δ (q,a) for some p,q ∈ Q, a ∈ T ∪ {λ}, then there is an edge from the circle representing state q to the circle representing state p and this edge is labeled by a. (Note that our graph concept is wider here than the usual digraph concept, since it allows multiple edges connecting two states, in most cases these multiple edges are drawn as normal edges having more than 1 labels.)
In this way, implicitly, the alphabet is also given by the graph (only those letters are used in the automaton which appear as labels on the edges).
In order to provide even more clarification, we present an example. We describe the same nondeterministic automaton both by a table and by a graph.
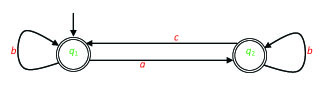
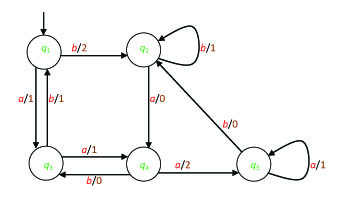
Example 21. Let an automaton be defined by the following Cayley table:
| T Q | → q0 | q1 | q2 | q3 |
|---|---|---|---|---|
| a | q1 | q1 | q2, q3 | - |
| b | q0 | q0 | - | q3 |
| c | q0 | q2 | - | q1,q2,q3 |
Figure 2.2. shows the graph representation of the same automaton.
These automata are used to accept words, and thus, languages:
Definition 16. (Language accepted by finite automaton). Let A = (Q, T, q0, δ, F) be an automaton and w ∈ T* be an input word. We say that w is accepted by A if there is a run of the automaton, i.e., there is an alternating sequence q0 t1 q1 ... qk-1 tk qk of states and transitions, that starts with the initial state q0, (qi ∈ Q for every i, they are not necessarily distinct, e.g., qi = qj is allowed even if i ≠ j) and for every of its transition ti of the sequence
ti : qi ∈ δ (qi-1,ai) in nondeterministic cases
ti : qi = δ (qi-1,ai) in deterministic cases,
where a1... ak = w, and qk ∈ F. This run is called an accepting run.
All words that A accepts form L(A), the language accepted (or recognized) by the automaton A.
Example 22. Let A be the automaton drawn in the next animations. We show a non-accepting run of a non-deterministic automaton A (with λ-transitions) in Animation 3.
However the word 1100 is accepted by A, since it has also an accepting run that is shown in Animation 4.
These finite automata are also called finite-state acceptors or Rabin-Scott automata. Let us see the language class(es) that can be accepted by these automata.
Two automata are equivalent if they accept the same language.
We have defined four types of finite automata and by the definition it seems that the latter ones are more restricted than the former ones. However, it turns out that all four versions characterize the same language class:
Theorem 4. For every finite automaton there is an equivalent (completely defined) deterministic finite automaton.
Proof. The proof is constructive. Let A = (Q, T, q0, δ, F) be a nondeterministic finite automaton (allowing λ-transitions). Let us define, first, the λ-closure of an arbitrary set q' of states.
let U1 ({q'}) = {q'},
let Ui+1 ({q'}) = Ui (q') ∪ {p ∈ Q∣∃r ∈ Ui (q') such that p ∈ δ (r,λ)}, for i > 1.
Since Q is finite, there is a value k such that Uk (q') = Uk+1 (q'), let us denote this set by U(q'). Practically, this set contains all the states that can be reached starting from a state of q' by only λ-transitions.
Now we are ready to construct the automaton A' =
(Q', T, U (q0), δ', F'), where Q'
= 2Q, F' ⊂ Q' includes every element
q' ∈ Q' such that q' ∩ F ≠ ∅. The transition
function δ' is defined as follows: 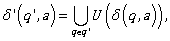 for any a ∈ T and q' ∈ Q'.
Actually while this can be done for all subsets of Q, subsets which cannot be reached by transitions from
U (q0) by δ' can be deleted (these
useless states are not needed).
for any a ∈ T and q' ∈ Q'.
Actually while this can be done for all subsets of Q, subsets which cannot be reached by transitions from
U (q0) by δ' can be deleted (these
useless states are not needed).
One can observe that A' is a completely defined deterministic automaton. Also, every run of A has an equivalent run of A', in fact, A' simulates every possible run of A on the input at the same time. Conversely, if A' has an accepting run, then A also has at least one accepting run for the same input. Therefore, A and A' accept the same language, consequently they are equivalent.
QED
Our previous proof gives an algorithm for the ''determinization'' of any finite automaton having only states reachable from the initial state as we will see it in details in Example 23. Note that even if we deleted these useless states, the automaton may not be minimal in the sense that the same language can be accepted by a completely defined deterministic finite automaton having less number of states than our automaton.
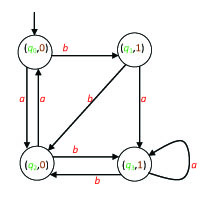
Example 23. Let a nondeterministic automaton be defined by the following Cayley table (note that in this algorithm the rows refer to the states of the automaton and the columns to the letters of the alphabet, and in this automaton λ-transitions are allowed):
| Q T | a | b | λ |
|---|---|---|---|
| → q0 | q0,q1 | q2 | - |
| q1 | q1 | - | q2 |
| q2 | q0 | q1 | - |
We start with the λ-closure of the initial state U (q0) = {q0}. This set will count as the initial state of the new automaton: let it be in the first row of the table of this new automaton. Let us see which sets of states can be obtained from this set by using the letters of the alphabet:
by letter a the set {q0, q1} is obtained, however, its λ-closure is {q0, q1, q2};
by letter b the set {q2} is obtained and its λ-closure is {q2}.
Let us write these two sets in the second and third row of the table. Now let us see what sets of states can be reached from these sets. First, let us see the set {q0, q1, q2}.
by letter a the set {q0, q1} is obtained, however, its λ-closure is {q0, q1, q2};
by letter b the set {q1, q2} is obtained and its λ-closure is {q1, q2}.
Since this latter set is not in the table yet, it is added to the fourth row. Now let us see the set {q2}.
by letter a the set {q0} is obtained, and its λ-closure is {q0};
by letter b the set {q1} is obtained and its λ-closure is {q1, q2}.
Since both of these two sets are already in the table we do not need to add a new row. Finally, let us analyse the set {q1,q2} (that is the last row of the table).
by letter a the set {q0, q1} is obtained, and its λ-closure is {q0, q1, q2};
by letter b the set {q1} is obtained and its λ-closure is {q1, q2}.
These sets are in the table. So the table is filled. The initial state of the new deterministic automaton is {q0}. The final states are: {q0, q1, q2}, {q2}, and {q1, q2}. The next table shows the resulting deterministic finite automaton:
| Q T | a | b |
|---|---|---|
| → {q0} | {q0, q1, q2} | {q2} |
| {q0, q1, q2} | {q0, q1, q2} | {q1, q2} |
| {q2} | {q0} | {q1, q2} |
| {q1, q2} | {q0, q1, q2} | {q1, q2} |
Example 24. Animation 5. shows an example how to obtain a completely defined deterministic automaton that is equivalent to the original nondeterministic automaton.
Let A = (Q, T, q0, δ, F) be a deterministic finite automaton such that each of its states is reachable from its initial state (there are no useless states). Then we can construct the minimal deterministic finite automaton that is equivalent to A in the following way:
Let us divide the set of states into two groups obtaining the classification C1 = {F, Q\F}. (We denote the class where state q is by C1[q].)
Then, for i > 1 the classification Ci is obtained from Ci-1: the states p and q are in the same class by Ci if and only if they are in the same class by Ci-1 and for every a ∈ T they behave similarly: δ (p,a) and δ (q,a) are in the same class by Ci.
Set Q is finite and, therefore, there is a classification Cm such that it is the same as Cm+1.
Then, we can define the minimal completely defined deterministic automaton that is equivalent to A: its states are the groups of the classification Cm, the initial state is the group containing the initial state of the original automaton, the final states are those groups that are formed from final states of the original automaton, formally:
(Cm, T, Cm [q0], δCm, FCm),
where δCm(Cm [q], a) = Cm [δ (q,a)] for every Cm [q] ∈ Cm, a ∈ T and FCm = {Cm [q]∣q ∈ F}.
It may happen that there are some words w ∈ T* that are not prefixes of any words of a regular language L. Then, the minimal completely defined deterministic automaton contains a sink state, that is the state where the word w and other words with the same property lead the automaton. When we want to have a minimal deterministic finite automaton for these languages, allowing partial (not completely defined) finite automata, then we may delete this sink state (with the transitions into it) by decreasing the number of the states by one.
Let us see yet another example. When applying the minimization algorithm it is more convenient to put the states to the 0th row of the table and the letters of the alphabet to the 0th column of the table.
Example 25. Let the deterministic automaton A be given as follows:
| T Q | → q0 | q1 | q2 | q3 | q4 | q5 | q6 |
|---|---|---|---|---|---|---|---|
| a | q2 | q5 | q1 | q1 | q2 | q1 | q0 |
| b | q1 | q0 | q3 | q4 | q5 | q3 | q2 |
Give a minimal deterministic automaton that is equivalent to A.
Solution:
Before applying the algorithm we must check which states can be reached from the initial state: from q0 one can reach the states q0, q2, q1, q3, q5, q4. Observe that the automaton cannot enter state q6, therefore, this state (column) is deleted. The task is to minimize the automaton
| T Q | → q0 | q1 | q2 | q3 | q4 | q5 |
|---|---|---|---|---|---|---|
| a | q2 | q5 | q1 | q1 | q2 | q1 |
| b | q1 | q0 | q3 | q4 | q5 | q3 |
by the algorithm. When we perform the first classification of the states C1 = {Q1, Q2} by separating the accepting and non-accepting states: Q1 = {q2, q4, q5}, Q2 = {q0, q1, q3} then we have:
| Q | Q1 | Q2 | |||||
|---|---|---|---|---|---|---|---|
| T | q2 | q4 | q5 | →q0 | q1 | q3 | |
| a | Q2 | Q1 | Q2 | Q1 | Q1 | Q2 | |
| b | Q2 | Q1 | Q2 | Q2 | Q2 | Q1 | |
Then C2 = {Q11, Q12, Q21, Q22} with Q11 = {q2, q5}, Q12 = {q4}, Q21 = {q0, q1}, Q22 = {q3}. Then according to this classification we have
| Q | Q11 | Q12 | Q21 | Q22 | |||
|---|---|---|---|---|---|---|---|
| T | q2 | q5 | q4 | →q0 | q1 | q3 | |
| a | Q21 | Q21 | Q11 | Q11 | Q11 | Q21 | |
| b | Q22 | Q22 | Q11 | Q21 | Q21 | Q12 | |
Since C3 = C2 we have the solution, the minimal deterministic finite automaton equivalent to A:
| T Q | Q11 | Q12 | →Q21 | Q22 |
|---|---|---|---|---|
| a | Q21 | Q11 | Q11 | Q21 |
| b | Q22 | Q11 | Q21 | Q12 |
We conclude this subsection by a set of exercises.
Exercise 17. Give a finite automaton that accepts the language of words that contain the consecutive substring baab over the alphabet {a,b}.
Exercise 18. Let the automaton A be given in a Cayley table as follows:
| T Q | →q0 | q1 | q2 | q3 | q4 |
|---|---|---|---|---|---|
| 0 | q0 | q1 | q2 | q4 | q1 |
| 1 | q1 | q2 | q3 | q3 | q4 |
Draw the graph of A. What is the type of A (e.g., nondeterministic with allowed λ-transitions)?
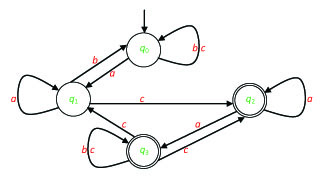
Exercise 19. The graph of the automaton A is given in Figure 2.3.
Describe A by utilizing a Cayley table. What is the type of A (e.g., deterministic with partially defined transition function)? What is the language that A recognizes?
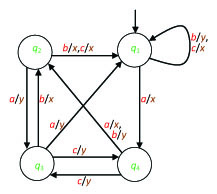
Exercise 20. Let a nondeterministic automaton with λ-transitions, A, be defined by the following Cayley table:
| Q T | a | b | c | λ |
|---|---|---|---|---|
| →q0 | q0, q3 | q1 | - | - |
| q1 | q1 | q3 | - | q2 |
| q2 | - | q0 | q2 | - |
| q3 | q1 | q1 | q2 | q0 |
Give a completely defined deterministic automaton that is equivalent to A.
Exercise 21. Let a nondeterministic automaton A be defined by the following table:
| Q T | 0 | 1 |
|---|---|---|
| →q0 | q0, q1 | q1 |
| q1 | q1 | q2, q3 |
| q2 | q0 | - |
| q3 | q3 | q0, q1, q2 |
Give a completely defined deterministic automaton that accepts the same language as A.
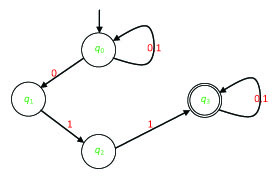
Exercise 22. Let a nondeterministic automaton A be defined by the graph shown in Figure 2.4.
Give a completely defined deterministic automaton that accepts the same language as A.
Exercise 23. Let the deterministic automaton A be given as follows:
| T Q | →q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 |
|---|---|---|---|---|---|---|---|---|
| a | q6 | q3 | q1 | q7 | q1 | q0 | q4 | q1 |
| b | q4 | q7 | q1 | q2 | q3 | q1 | q5 | q6 |
| c | q5 | q2 | q6 | q1 | q3 | q6 | q0 | q6 |
Give a minimal deterministic automaton that is equivalent to A.
Exercise 24. Let the deterministic automaton A be given by the following table.
| T Q | →q0 | q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 |
|---|---|---|---|---|---|---|---|---|---|
| 0 | q3 | q5 | q7 | q0 | q2 | q0 | q4 | q2 | q5 |
| 1 | q8 | q1 | q3 | q2 | q6 | q7 | q3 | q5 | q2 |
Give a minimal deterministic automaton that is equivalent to A. (Hint: check first which states can be reached from the initial state.)
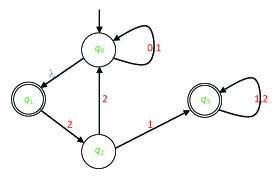
Exercise 25. Let a nondeterministic automaton A be defined by the graph shown in Figure 2.5.
Give a minimal deterministic automaton that is equivalent to A.
Now we are going to show that exactly the class of regular languages can be described with the help of the finite automata. First we show that every regular language (type 3 language) can be accepted by finite automata.
Theorem 5. Every language generated by a regular grammar is accepted by a finite automaton.
Proof. The proof is constructive. Let G = (N, T, S, P) be a regular grammar in normal form. Then, let the finite automaton
A = (Q, T, q0, δ,F)
be defined as follows:
let Q = N ∪ {F'} (where F' ∉ N),
q0 = S.
Let the transition function δ be defined by the elements of P: let B ∈ δ (A,a) if A → aB ∈ P; and let F' ∈ δ (A,a) if A → a ∈ P. Further, let the set of accepting states be {F'} if S →λ is not in P and let F = {F',S} if S → λ ∈ P.
One can see that the successful derivations in the grammar and the accepting runs of the automaton have a one-to-one correspondence.
QED.
G = ({S, A, B, C}, {a, b, c}, S,
{ S → abbA,
S → baaB,
S → λ,
A → aS,
A → aC,
B → bC,
C → aS,
C → cc
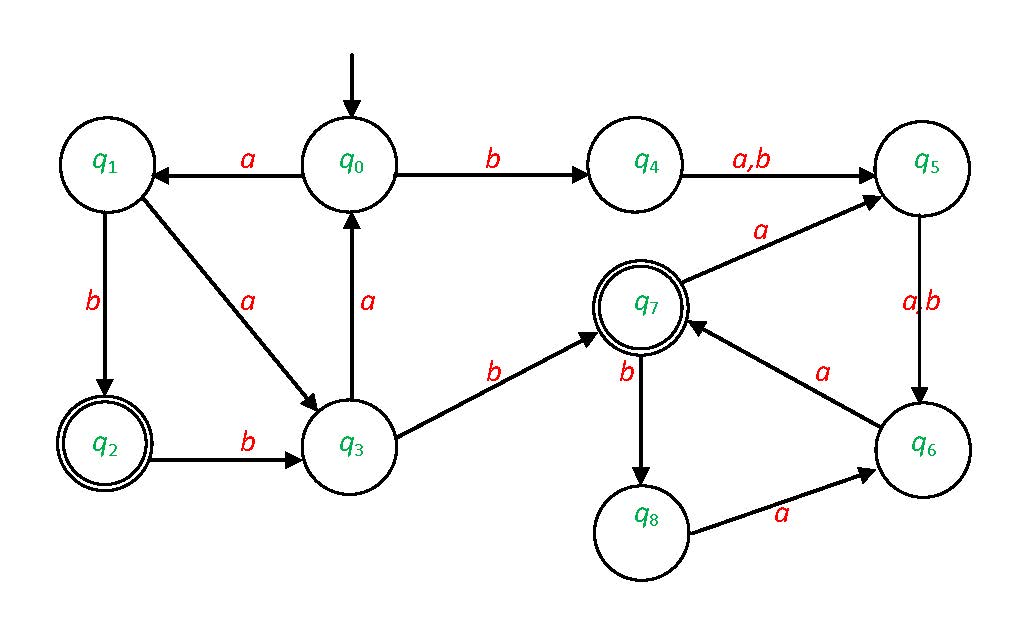
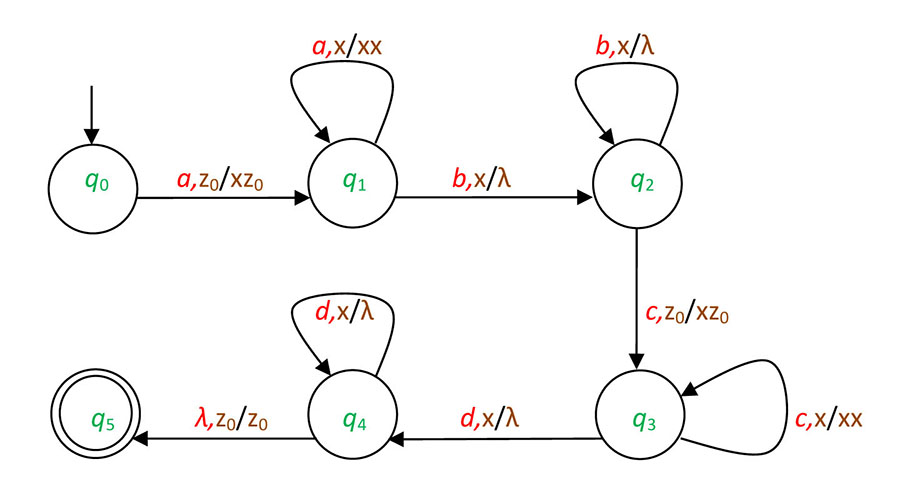
}) generating the language L(G). Give a finite automaton that accepts the language L(G).
Solution:
First we must exclude the rules containing more than 1 terminals, as we did in the proof of Theorem 2. In this way the grammar
G' =({S, A, B, C, X1, X2, X3, X4, X5}, {a, b, c}, S,
{ S → aX1,
X1 → bX2,
X2 → bA,
S → bX3,
X3 → aX4,
X4 → aB,
S → λ,
A → aS,
A → aC,
B → bC,
C → aS,
C → cX5,
X5 → c
}) can be obtained. Then, we can draw the graph of automaton A as it can be seen in Figure 2.6.
Now we are going to show that the class of finite automata cannot accept more languages than the class that can be described by regular expressions.
Theorem 6. Every language accepted by a finite automaton can be described by a regular expression.
Proof. The proof is constructive. We present an algorithm that shows how one can construct a regular
expression from a finite automaton. We can restrict ourselves to deterministic finite automaton, since we have already seen that they
are equivalent to the nondeterministic finite automata. Let the states of a deterministic finite automaton be 1,2,... for the sake of simplicity, i.e.,
let A = ({1,... n}, T, 1, δ, F) be given.
Let 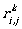 denote the regular expression that describes the language accepted by the automaton
({1,...,k} ∪ {i,j}, T, i, δ', {j}),
where δ' is the restriction of δ
containing only transitions from the set {i} ∪ {1,...,k} to the set
{1,...,k} ∪ {j} (1 ≤ i,j ≤ n,
0 ≤ k ≤ n and 1,..., 0 means the empty set).
denote the regular expression that describes the language accepted by the automaton
({1,...,k} ∪ {i,j}, T, i, δ', {j}),
where δ' is the restriction of δ
containing only transitions from the set {i} ∪ {1,...,k} to the set
{1,...,k} ∪ {j} (1 ≤ i,j ≤ n,
0 ≤ k ≤ n and 1,..., 0 means the empty set).
Then, 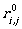 describes the regular language that is given by direct transition(s) from state
i to j.
Therefore,
describes the regular language that is given by direct transition(s) from state
i to j.
Therefore, 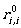 gives the language {λ} ∪ {a∣δ (i,a) = i}
(this language contains the empty word and possibly some one-letter-long words, i.e., it is
described by a basic regular expression or
finite union of basic regular expressions).
gives the language {λ} ∪ {a∣δ (i,a) = i}
(this language contains the empty word and possibly some one-letter-long words, i.e., it is
described by a basic regular expression or
finite union of basic regular expressions).
Further, 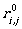 describes the language {a∣δ (i,a) = j}
if i ≠ j (it can contain some one-letter-long words).
These regular expressions can easily be obtained and proven to describe the languages mentioned.
describes the language {a∣δ (i,a) = j}
if i ≠ j (it can contain some one-letter-long words).
These regular expressions can easily be obtained and proven to describe the languages mentioned.
Now we use induction on the upper index:
for 1 ≤ k ≤ n.
This expression can be seen intuitively: starting from state i we could reach state j by using
the first k states in our path, either without using state k (the part 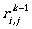 refers
to this case) or by a path reaching state
refers
to this case) or by a path reaching state 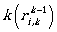 , and then reaching it arbitrarily
many times (including 0 times:
, and then reaching it arbitrarily
many times (including 0 times: 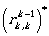 , and finally reaching state j from state
, and finally reaching state j from state 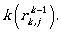
Finally, 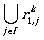 gives a regular expression that describes exactly the
language accepted by A.
In this way it is constructively proven that for any finite automaton one can construct a regular
expression that describes the
language accepted by the automaton.
gives a regular expression that describes exactly the
language accepted by A.
In this way it is constructively proven that for any finite automaton one can construct a regular
expression that describes the
language accepted by the automaton.
QED.
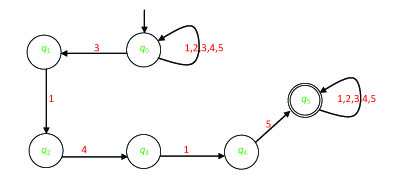
Example 27. Let the Cayley table of automaton A be given as follows:
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| a | q2 | q3 | q1 |
| b | q3 | q2 | - |
Describe the accepted language L(A) by a regular expression.
Solution:
Let us describe the regular expressions 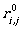 for i,j ∈ {1,2,3} by using the transitions of A.
for i,j ∈ {1,2,3} by using the transitions of A.
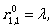 | 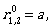 | 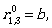 |
 | 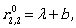 | 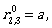 |
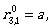 | 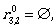 | 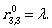 |
Now by using the inductive step we compute 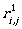 for i,j ∈ {1,2,3}.
for i,j ∈ {1,2,3}.
Now we can continue by computing the expressions 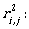
To describe L(A) we need 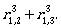 Let us compute it:
Let us compute it:
Thus, the regular expression
(ab*a + b)(aab*a + ab)* aab* + ab* + (ab*a + b)(aab*a + ab)* = (ab*a + b)(aab*a + ab)* (λ + aab*) + aab*
describes L(A). The problem is solved.
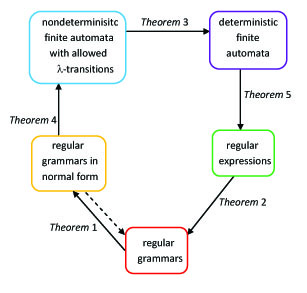
Now we have proven that the three concepts we have discussed in this chapter, the regular grammars, regular expressions and finite automata are equivalent in the sense that each of them characterize exactly the class of regular languages (see Figure 2.7).
Figure 2.7. The equivalence of the three types of descriptions (type-3 grammars, regular expressions and finite automata) of the regular languages.
 |
The aim of the analysis of a finite automaton is the task to describe the accepted language in another way, usually, by regular expressions. The synthesis of a finite automaton is the construction of the automaton that accepts a regular language that is usually given by a regular expression. Kleene has proven the equivalence of finite automata and regular expressions.
The minimization algorithm is very important, since the minimal, completely defined, deterministic finite automaton is (the only known) unique identification of a regular language. In this way, we can decide if two regular languages (given by regular expressions, grammars or automata) coincide or not.
We close this subsection by a set of exercises.
Exercise 26. Let
G = ({S, A, B}, {0,1}, S,
{ S → 000A,
S → 111B,
A → λ,
A → 0S,
A → 11,
B → 1S,
B → 000
}) generating language L(G). Give a finite automaton that accepts language L(G). (Hint: first transform the grammar to normal form.)
Exercise 27. Let
G = ({S, A, B, C}, {a,b}, S,
{ S → aaaA,
S → bbB,
S → C,
A → S,
A → baB,
A → ba,
B → S,
B → C,
B → b,
B → λ,
C → B,
C → aA
}) generating language L(G). Give a finite automaton that accepts language L(G).
Exercise 28. Let
G = ({S, A, B}, {a, b, c}, S,
{ S → abA,
S → bccS,
A → bS,
A → c,
A → B,
B → S,
B → aA,
B → bcc,
B → λ
}) generating language L(G). Give a finite automaton that accepts language L(G).
Exercise 29. Let the automaton A be defined by the following table:
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| 0 | q1 | q3 | q3 |
| 1 | q2 | q2 | q1 |
Give a regular expression that describes the language accepted by automaton A.
Exercise 30. Let automaton A, accepting language L(A), be defined by the Cayley table:
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| a | q1 | q3 | - |
| b | - | q2 | q1 |
| c | q2 | q2 | - |
Give a regular expression that describes language L(A).
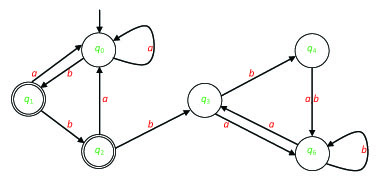
Exercise 31. Let automaton A be as it is shown in Figure 2.8. Give a regular expression that defines the same language as A.
The word problem is to decide whether any given word w belongs to a given regular language (or not). This can be done very efficiently by using a deterministic finite automaton that accepts the given language. (Such an automaton can be constructed from a regular expression, first by Theorem 3. and then/or from a grammar by Theorem 5. and then/or from a nondeterministic finite automaton by Theorem 4.) Reading the word w can be done by ∣w∣ steps, and then, if the automaton accepts w, i.e., it arrived at an accepting state in this run, then w is an element of the language. Otherwise, (if there were some undefined transitions and the automaton gets stuck, or by reading the word finally a non accepting state is reached) w does not belong to the given regular language. The decision on an input word of length n is done in at most n steps, therefore, this is a real time algorithm (i.e., linear time algorithm with coefficient 1). There is no faster algorithm that can read the input, so the word problem for regular languages can be solved very efficiently.
Exercise 32. Let automaton A be given as it can be seen in Figure 2.9.
Decide whether the words
abab,
baba,
aaaabbb,
bbbaaaab,
baabaabaabb and
aaaabbbababaaa are in L(A).
Exercise 33. Let the nondeterministic automaton A be defined by the Cayley table:
| T Q | 0 | 1 | λ |
|---|---|---|---|
| →q0 | q1, q4 | q5 | q2 |
| q1 | q3 | q1, q4 | - |
| q2 | q1 | q2 | - |
| q3 | - | - | q2 |
| q4 | - | q4 | - |
| q5 | q5 | q5 | q0 |
Decide which of the words 0011, 0101, 0110, 01110010, 100, 1011110 belong to the accepted language of A.
Exercise 34. Let
G = ({S, A, B}, {a, b, c}, S,
{ S → abcS,
S → bcA,
S → acB,
A → aS,
A → a,
B → bS,
B → bcc,
S → ccc
}) be a regular grammar. Decide which of the following words can be generated by G:
abcccc,
acbcc,
acbbacbccc,
bca,
bcacacc,
bcaabcacbcc,
ccc,
cccacbc.
Exercise 35. Given the regular language
a* + (a+b)*baba (a+b)*),
decide if the following words are in the described language or not:
aaaaa,
aaabaa,
ababa,
abbabaaba.
In the next part of this section we concentrate on the closure properties of the class of regular languages.
By the constructive proof of Theorem 3, it is also shown that the class of regular languages is closed under the regular operations. Now let us consider the set theoretical operations: intersection and complement.
Theorem 7. The class of regular languages is closed under intersection and complement.
Proof. The proof is constructive in both cases, and deterministic finite automata are used.
Let us start with the complement. Let a regular language be given by a complete deterministic
finite automaton A = (Q, T, q0, δ, F) that recognizes it.
This automaton has exactly one run for
every word of T*, and accepts a word if this run is finished in an accepting state.
Then 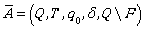 recognize exactly those words that are not accepted
by A, and thus the finite automaton
recognize exactly those words that are not accepted
by A, and thus the finite automaton 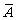 accepts the complement of the original regular language.
accepts the complement of the original regular language.
For the intersection, let two regular languages L1 and L2 be given by complete deterministic automata A = (Q, T, q0, δ,F) and A' = (Q', T, q'0, δ', F') that recognize them, respectively. Then, let A∩ = (Q × Q', T, (q0, q'0), δ'', F× F'), with transition function δ'' ((q,q'), a) = (δ(q,a), δ' (q',a)) for every q ∈ Q, q' ∈ Q' and a ∈ T. The states are formed by pairs of the states of the automata A and A'. Thus, A∩ simulates the work of these two automata simultaneously and accepts exactly those words that are accepted by both of these machines. Thus the intersection of the languages L1 and L2 is accepted by a finite automaton, and thus it is also a regular language.
QED.
Example 28. Let the automaton A and A' accept the languages L(A) and L(A'), respectively. Let them be defined in the following way: the table of A as shown below.
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| a | q3 | q2 | q3 |
| b | q2 | q2 | q3 |
the table of A' as shown below
| T Q' | →q'1 | q'2 |
|---|---|---|
| a | q'1 | q'1 |
| b | q'2 | q'2 |
Give an automaton that accepts the complement of L(A) and an automaton that accepts the intersection of L(A) and L(A'). What are the languages accepted by these automata?
Solution:
Let us take the automaton that accepts the complement of L(A) by interchanging the role of
accepting and non-accepting states in A. Let 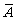 be defined by the following Cayley table:
be defined by the following Cayley table:
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| a | q3 | q2 | q3 |
| b | q2 | q2 | q3 |
Now let us construct A∩ by using the Cartesian product of the sets of states Q and Q'.
| T Q | →(q1, q'1) | (q2, q'1) | (q3, q'1) | (q1, q'2) | (q2, q'2) | (q3, q'2) |
|---|---|---|---|---|---|---|
| a | (q3, q'1) | (q2, q'1) | (q3, q'1) | (q3, q'1) | (q2, q'1) | (q3, q'1) |
| b | (q2, q'2) | (q2, q'2) | (q3, q'2) | (q2, q'2) | (q2, q'2) | (q3, q'2) |
Actually, A accepts the language a(a+b)* (words starting by letter a),
and A' accepts the language (a+b)* b
(words that ends with letter b), the automaton 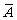 accepts the language λ + b(a+b)
* (words do not start with letter a over the alphabet {a,b}),
while A∩ accepts the
language a (a+b)* b (words starting with a and ending with b).
accepts the language λ + b(a+b)
* (words do not start with letter a over the alphabet {a,b}),
while A∩ accepts the
language a (a+b)* b (words starting with a and ending with b).
Exercise 36. Let the table of A be
| T Q | →q1 | q2 | q3 |
|---|---|---|---|
| 0 | q1 | q3 | q2 |
| 1 | q2 | q2 | q2 |
and the table of A' be
| T Q' | →q'1 | q'2 | q'3 |
|---|---|---|---|
| 0 | q'3 | q'2 | q'3 |
| 1 | q'2 | q'1 | q'2 |
Give an automaton that accepts the intersection of the languages accepted by A and A'.
Exercise 37. Let the language L(A) be defined as the accepted language of the automaton A as it is shown in Figure 2.10.
Give an automaton that accepts the complement of L(A). (Hint: first the equivalent completely defined deterministic automaton must be obtained.)
Exercise 38. Let the table of A be
| T Q' | →q1 | q2 | q3 | q4 |
|---|---|---|---|---|
| a | q1 | q3 | q1 | q1 |
| b | q1 | q4 | q2 | q2 |
| c | q2 | q4 | q4 | q3 |
and the table of A' be
| T Q' | →q'1 | q'2 |
|---|---|---|
| a | q'1 | q'2 |
| b | q'2 | q'1 |
| c | q'2 | q'1 |
They accept the languages L(A) and L(A'), respectively.
Give automata that accept the complement of L(A) and L(A'). Give an automaton that accepts L(A) ∩ L(A').
In the next part we show an if and only if characterization of the class of regular languages.
Let us define congruence relations on T* with the following property: for every u, v, w ∈ T* if u ∼ v, then uw ∼ vw. These relations are called right-congruences. A congruence relation is of finite index, if the number of classes of T* is finite.
Theorem 8. (Myhill-Nerode theorem). A language over the alphabet T is regular if and only if there is a finite index right-congruence relation on T* such that the language is obtained as (the union of) some of the classes induced by the relation.
Let a language L be given. Roughly speaking two words, u and v are equivalent if their every possible continuation w behaves in the same manner, i.e., uw ∈ L if and only if vw ∈ L. If this equivalence relation induces finitely many classes on T*, then, and only then, L is regular.
Actually, this fact is also related to the minimal, completely defined, accepting deterministic finite automaton (that uniquely identifies the given regular language): the partitions of T* can be assigned to the states of the minimal automaton: the partition containing the empty word λ is assigned to the initial state; those partitions that contain words such that their empty continuation is in L are assigned to the accepting states. The transitions can also be easily defined by using the partitions, by checking in which partition the words are that are given by the previous one by extending it with exactly one letter.
Now, we are going to give an example for how this theorem can be used to show that some of the languages are not regular.
Example 29. Let us analyze language L = {an bn∣n ∈ ℕ}. Let us partition the words of a* into classes: assume that ak and am are in the same class, i.e., ak ∼ am. Then, for each possible continuation (w ∈ {a,b}*) they behave in the same manner, e.g., for bk the word akbk ∈ L and thus, ambk ∈ L also. But it can only be if m = k, and so every element of a* is equivalent to only itself and not to any other element of this set. Therefore, language L induces an infinite index right-congruence relation, thus L is not regular.
Exercise 39. Show that the language containing exactly the words having the same number of 0's and 1's (over the alphabet {0,1}) is not regular.
(Apply the Myhill-Nerode theorem.)
Exercise 40. Show that the language L = {an2∣n ∈ ℕ} (over the alphabet {a}), i.e., the unary words having square number length, is not regular.
(Apply the Myhill-Nerode theorem.)
Transducers are machines which do not only have input, but output as well. One can imagine them as automata with two tapes: an input and an output tape. In this book, we consider only the simplest transducers: they are finite and they give an output letter as a response to every input letter. In this section, we briefly describe two types of finite state transducers.
We start by giving the formal definition of Mealy automata.
Definition 17. A Mealy automaton is an ordered sextuple A = (Q, T, V, q0, δ, μ), where Q, T, q0, δ are the same as at the completely defined deterministic finite state acceptors, i.e., Q is the finite set of states, T is the input alphabet, q0 ∈ Q is the initial state, δ : Q × T → Q is the transition function; and V is the output alphabet and μ : Q × T → V is the output function.
Notice that there are no final (or accepting) states. These automata are not used to accept languages.
A Mealy automaton can be defined by a Cayley table or by a graph. When a Cayley table is used to describe a Mealy automaton, then both the values δ(q,a) and μ(q,a), as pairs are written to the cell identified by the state q and by the letter a. When a graph is used to describe a Mealy automaton, then we can put a/x to an arrow meaning that the transition represented by the arrow is performed by reading an input letter a, while an output letter x ∈ V is written to the output tape. Here is an example.
Example 30. Let the Mealy automaton A be given by the following Cayley table
| T Q | →q1 | q2 | q3 | q4 |
|---|---|---|---|---|
| a | (q4, x) | (q3, y) | (q1, y) | (q2, x) |
| a | (q1, y) | (q1, x) | (q2, x) | (q2, y) |
| a | (q1, x) | (q1, x) | (q4, y) | (q3, y) |
The same automaton given by graph can be seen in Figure 2.11.
Let us make some sample runs of the automaton:
Let the input be abcabc, then the output is xyxxyx.
Let the input be aaaabbbb, then the output is xxyyyyyy.
Let the input be ccabcabc, then the output is xxxyxxyx.
Let the input be abcbbccabac, then the output is xyxyyxxxyyy.
Example 31. Animation 6. shows an example of a Mealy automaton, how it produces output for a given input.
We say that two Mealy automata are equivalent if they assign the same output word for every input word u ∈ T*. The number of states of equivalent automata can be various. However, there is particular Mealy automaton for each equivalent class that has a minimal number of states. This automaton can be obtained from any automaton of the class by the minimization algorithm.
Now we present the minimization algorithm for Mealy automata. First, as with the finite state recognizers, we should check which states can be reached from the initial state. The states that cannot be reached can simply be erased from the automaton (table or graph) together with the transitions from them.
When we have a Mealy automaton, such that each of its states is reachable from the initial state with some input words (i.e., reading the given input word the automaton arrives to this particular state), then we can start an analogous algorithm that was used for minimizing finite state recognizers.
Only the initial step of the algorithm differs from the one shown previously: since we have no accepting states, the initial classification is done in another way. Let two states p and q be in the same class, i.e., C1[p] = C1[q] if and only if for every input letter a ∈ T the equality μ(p,a) = μ(q,a) is fulfilled.
The other steps of the algorithm are similar to the previously described algorithm: based on the previous classification the next classification is obtained by separating those states for which there is an input letter such that the transition function with this letter brings them to different classes.
Let us see an example.
Example 32. Let the Mealy automaton A be given as follows:
| T Q | →q1 | q2 | q3 | q4 | q5 | q6 |
|---|---|---|---|---|---|---|
| a | (q2, x) | (q1, z) | (q6, x) | (q5, z) | (q4, x) | (q5, x) |
| b | (q3, y) | (q2, y) | (q4, y) | (q4, y) | (q3, y) | (q2, y) |
Give the minimal Mealy automaton that is equivalent to A.
Solution:
One can easily check that every state can be reached from the initial state. Then classification C1 = {Q1, Q2}, where Q1 = {q1, q3, q5, q6} (having output x for input a and output y for input b) and Q2 = {q2, q4} (having output z for input a and output y for input b). Then, the transition function reflecting this classification is as follows:
| Q | Q1 | Q2 | |||||
|---|---|---|---|---|---|---|---|
| T | →q1 | q3 | q5 | q6 | q2 | q4 | |
| a | Q2 | Q1 | Q2 | Q1 | Q1 | Q1 | |
| b | Q1 | Q2 | Q1 | Q2 | Q2 | Q2 | |
Then, Q1 is divided into two subgroups in the classification C2 = {Q11, Q12, Q2} with Q11 = {q1, q5} and Q12 = {q3, q6}. (Q2 = {q2, q4} remains the same group.) The transition function reflecting these groups is as follows:
| Q | Q11 | Q12 | Q2 | ||||
|---|---|---|---|---|---|---|---|
| T | →q1 | q5 | q3 | q6 | q2 | q4 | |
| a | Q2 | Q2 | Q11 | Q12 | Q11 | Q11 | |
| b | Q12 | Q12 | Q2 | Q2 | Q2 | Q2 | |
Only Q12 is divided (to its elements) and thus C3 = {Q11, Q121, Q122, Q2} with Q121 = {q3} and Q122 = {q5}. Then the transitions become:
| Q | Q11 | Q121 | Q122 | Q2 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| T | →q1 | q5 | q3 | q6 | q2 | q4 | ||||||
| a | Q2 | Q2 | Q11 | Q122 | Q11 | Q11 | ||||||
| b | Q121 | Q121 | Q2 | Q2 | Q2 | Q2 | ||||||
Since C4 = C3, we can give the minimal Mealy automaton (writing also the values of the output function into the table):
| T Q | →Q11 | Q121 | Q122 | Q2 |
|---|---|---|---|---|
| a | (Q2, x) | (Q11, x) | (Q122, x) | (Q11, z) |
| b | (Q121, y) | (Q2, x) | (Q2, y) | (Q2, y) |
Exercise 41. Let the Mealy automaton A be given with its table as follows:
| T Q | →q0 | q1 | q2 | q3 |
|---|---|---|---|---|
| 0 | (q0, a) | (q3, a) | (q1, b) | (q2, b) |
| 1 | (q1, b) | (q1, a) | (q2, b) | (q2, a) |
Draw the graph of automaton A.
Exercise 42. Let the Mealy automaton A be given by its graph as it is shown in Figure 2.12.
Describe the same automaton with a Cayley table.
What is the output of this automaton for the input strings aaabb, abbba, bbbaabb and aabbbaabab?
Give a minimal Mealy automaton that is equivalent to A.
Exercise 43. Give a minimal Mealy automaton that is equivalent to the following one:
| T Q | →q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 |
|---|---|---|---|---|---|---|---|---|
| a | (q8, 0) | (q3, 1) | (q8, 0) | (q1, 1) | (q8, 0) | (q4, 0) | (q3, 1) | (q5, 1) |
| b | (q2, 1) | (q1, 0) | (q7, 0) | (q2, 1) | (q7, 1) | (q2, 1) | (q6, 0) | (q3, 1) |
Exercise 44. Give a minimal Mealy automaton that is equivalent to the one defined by the following table.
| T Q | →q1 | q2 | q3 | q4 | q5 |
|---|---|---|---|---|---|
| a | (q2, x) | (q2, y) | (q2, x) | (q5, y) | (q4, y) |
| b | (q4, x) | (q3, x) | (q1, x) | (q3, x) | (q3, x) |
| c | (q5, y) | (q5, x) | (q1, y) | (q5, x) | (q2, x) |
In this subsection another type of finite transducers are investigated.
Definition 18. A Moore automaton is an ordered sextuple A = (Q, T, V, q0, δ, η), where Q, T, V, q0, δ are the same as at the Mealy automata, and η : Q × V is the output function.
Notice that the difference between the Mealy and the Moore automata is due to their output function. While with the Mealy automata the output is produced during the transition (depending on both the state that the automaton was in and on the read input letter), at the Moore automata the output letter is produced after the transition is finished and the output letter depends only on the state the automaton reached by the transition.
The Moore automata can also be defined by Cayley table and by graph. Since with the Moore automata the output depends only on the state the automaton has reached, the output letters are written to the states (above the states, when the states are in the 0th row of table) and inside the circles of the states as pairs containing the state and the output assigned to the state on the graphs. Here is an example:
Example 33. Let the Moore automaton A be given by its graph as it is shown in Figure 2.13.
Describe the same automaton using a Cayley table. Give the output for input strings
aabb,
baabaa and
abaababb.
Solution:
| V | 0 | 1 | 0 | 1 |
|---|---|---|---|---|
| T Q | →q0 | q1 | q2 | q3 |
| a | q2 | q3 | q0 | q3 |
| b | q1 | q2 | q3 | q2 |
The example runs give the outputs as follows:
For input aabb the output is 0010.
For input baabaa the output is 111000.
For input abaababb the output is 01110010.
Example 34. Animation 7. shows a Moore automaton at work.
Now we can generalize the equivalence relation between finite transducers: a Mealy/Moore automaton A is equivalent to a Mealy/Moore automaton A' if and only if for every input string u ∈ T* they produce the same output string.
The Moore automata can also be minimized and its algorithm is very similar to the previously described minimization algorithms. The only difference is that in this case the first classification is done based on the output letters assigned to the states, i.e., the states p and q are in the same class by classification C1 if and only if η(p) = η(q).
Let us see an example of how the algorithm works for the Moore automata.
Example 35. The Moore automata A is defined by its Cayley table as follows:
| V | x | y | y | y | x | x | x |
|---|---|---|---|---|---|---|---|
| T Q | →q1 | q2 | q3 | q4 | q5 | q6 | q7 |
| a | q2 | q5 | q1 | q5 | q2 | q3 | q4 |
| b | q7 | q4 | q6 | q2 | q4 | q6 | q1 |
Find a minimal Moore automaton that is equivalent to A.
Solution:
First we check if every state is reachable from the initial state. It can be seen that states q3 and q6 are not reachable, therefore we erase them. We need to minimize the automaton
| V | x | y | y | x | x |
|---|---|---|---|---|---|
| T Q | →q1 | q2 | q4 | q5 | q7 |
| a | q2 | q5 | q5 | q2 | q4 |
| b | q7 | q4 | q2 | q4 | q1 |
Classification C1 = {Q1, Q2} is based on the output function: Q1 = {q1, q5, q7} (having output x) and Q2 = {q2, q4} (having output y). Then, the transitions using the classification become:
| Q | Q1 | Q2 | ||||
|---|---|---|---|---|---|---|
| T | →q1 | q5 | q7 | q2 | q4 | |
| a | Q2 | Q2 | Q2 | Q1 | Q1 | |
| b | Q1 | Q2 | Q1 | Q2 | Q2 | |
Then, Q1 is divided into two subclasses, therefore C2 = {Q11, Q12, Q2} where Q11 = {q1, q7} and Q12 = {q5}. Then, we have:
| Q | Q11 | Q12 | Q2 | |||
|---|---|---|---|---|---|---|
| T | →q1 | q7 | q5 | q2 | q4 | |
| a | Q2 | Q2 | Q2 | Q12 | Q12 | |
| b | Q11 | Q11 | Q2 | Q2 | Q2 | |
Thus C3 = C2, and we can describe the minimal Moore automaton as follows:
| V | x | x | y |
|---|---|---|---|
| T Q | →Q11 | Q12 | Q2 |
| a | Q2 | Q2 | Q12 |
| b | Q11 | Q2 | Q2 |
We note here that the minimization methods for finite automata presented in this book are using the Aufenkamp-Hohn algorithm.
Exercise 45. A Moore automaton A is given by the following Cayley table:
| V | x | x | y | z | z | y |
|---|---|---|---|---|---|---|
| T Q | →q0 | q1 | q2 | q3 | q4 | q5 |
| a | q4 | q5 | q3 | q0 | q4 | q5 |
| b | q1 | q2 | q4 | q5 | q5 | q5 |
Give the same automaton by a graph. What is the output of the automaton for the input words
abbaab and
bbaabbaabbbb?
Exercise 46. The Moore automaton A is defined by the graph shown in Figure 2.14.
Give it by a Cayley table. Give its output for the input
cabbaccc,
aabbccabcabcbbcaca and
acaabacbbbcccaa.
Exercise 47. The Moore automata A is defined by its Cayley table as follows:
| V | 0 | 1 | 0 | 2 | 0 | 2 | 0 | 1 | 1 |
|---|---|---|---|---|---|---|---|---|---|
| T Q | →q1 | q2 | q3 | q4 | q5 | q6 | q7 | q8 | q9 |
| a | q1 | q5 | q8 | q5 | q9 | q1 | q2 | q3 | q3 |
| b | q2 | q4 | q6 | q2 | q6 | q8 | q4 | q5 | q1 |
| c | q3 | q9 | q8 | q2 | q8 | q8 | q7 | q6 | q8 |
Find a minimal Moore automaton that is equivalent to A.
Exercise 48. The Moore automata A is defined by its Cayley table as follows:
| V | x | y | y | y | z | z |
|---|---|---|---|---|---|---|
| T Q | →q1 | q2 | q3 | q4 | q5 | q6 |
| a | q2 | q4 | q4 | q2 | q2 | q3 |
| b | q3 | q2 | q6 | q4 | q6 | q5 |
Give the minimal Moore automaton that is equivalent to A.
Finally, we devote this subsection to a brief analysis of the mappings T* → V* that can be obtained by the Mealy and the Moore automata.
We provide a theorem that the classes of the Mealy and the Moore automata have the same efficiency.
Theorem 9. (Gill's theorem). For every Mealy automaton there exists an equivalent Moore automaton and for every Moore automaton there exists an equivalent Mealy automaton.
For a Moore automaton there is a very simple way to construct a Mealy automaton that defines the same mapping from T* to V*. Roughly speaking, the output letter should move from a state to each of the transitions (arrows in the graph) into the given state. The other direction, that is not detailed here, can be done my multiplying the number of states (using the set Q × V).
Now let us see some of the important properties of the mappings that can be defined by finite transducers.
Theorem 10. (Raney's theorem). The automata mappings have the following two properties:
They are length preserving, i.e., for any input string w ∈ T* its length is the same as the length of the output u ∈ V* given by w.
They are prefix keeping, i.e., the image of the prefix will also be prefix, more formally: for every w,v ∈ T* the output for the string wv will start with the output string assigned to w.
We note here that there are automata mappings that cannot be defined by the finite state Mealy or Moore automata, but only by their infinite state variants. We have chosen not to discuss these infinite variants in our book.
Summary of the chapter: In this chapter, we deal with a family of languages between the regular and context-free languages of the Chomsky hierarchy, i.e., the linear languages. We give an example for a non-regular linear language. A normal form for linear grammars is proven. The class of one-turn pushdown automata recognizes exactly the class of linear languages. This class is closed under union, but it is not closed under concatenation, Kleene-star, complement and intersection.
First let us recall the definition of linear grammars.
Definition 19. (Linear grammars). A grammar G = (N, T, S, P) is linear if each of its productions has one of the following forms: A → u, A → uBv, where A,B ∈ N, u,v ∈ T*. The languages that can be generated by linear grammars are the linear languages.
This class of languages are between the (classes of) type 3 and type 2 languages of the Chomsky hierarchy, thus we may call them type 2.5 languages. The linear grammars inherit the property of the regular grammars that there is at most one nonterminal in any sentential form. However, this nonterminal is not restricted to be at the end of the sentential form (as it was in the regular case), it can be in an arbitrary place.
Now, we give an example, where the nonterminal is in the middle of the sentential forms in every derivation.
G = ({S}, {a,b}, S, {S → aSb, S →λ}).
Then, every (finished) derivation in this grammar has the following form: applying the first rule n times (n ∈ ℕ, n ≥ 0) and then applying the second rule. Hence, the generated language is {anbn∣n ∈ ℕ}. See also Animation 8. for an example derivation in this grammar.
Remember that in Example 29. we have shown that this language is not regular, and thus, with Example 36 we have just proven that the class of linear languages strictly includes the class of regular languages.
Theorem 11. Every linear language can be generated by a grammar having productions in the following forms, only:
A → aB, A → Ba, A → a, S→λ.
(We call a grammar with this property a linear grammar in normal form.)
Proof. The proof is constructive. Given G = (N, T, S, P) a linear grammar, we show how one can construct a grammar G' that is in normal form and equivalent to G.
If there is a (are) rule(s) of the form A → λ (A ≠ S), then first the Empty-word lemma (Theorem 1.) is applied and grammar G'' = (N'', T, S', P'') is obtained that may only contain λ in the right hand side of the rule S' → λ. Then in G'' either S = S', N'' = N or S' ∉ N and in this latter case N'' = N ∪ {S'}.
Now as an intermediate step, we replace each of the rules A → uBv (where u ≠ λ, v ≠ λ) with rules A → uX, X → Bv, where X is a newly introduced nonterminal, i.e., X ∉ N''. After the substitution of each rule of this form grammar G''' = (N''', T, S', P''') is obtained and it is equivalent to the original grammar G. (See the left side of Figure 3.1., for an example.)
Figure 3.1. In derivations the rules with long right hand side (left) are replaced by chains of shorter rules in two steps, causing a binary derivation tree in the resulting grammar (right).
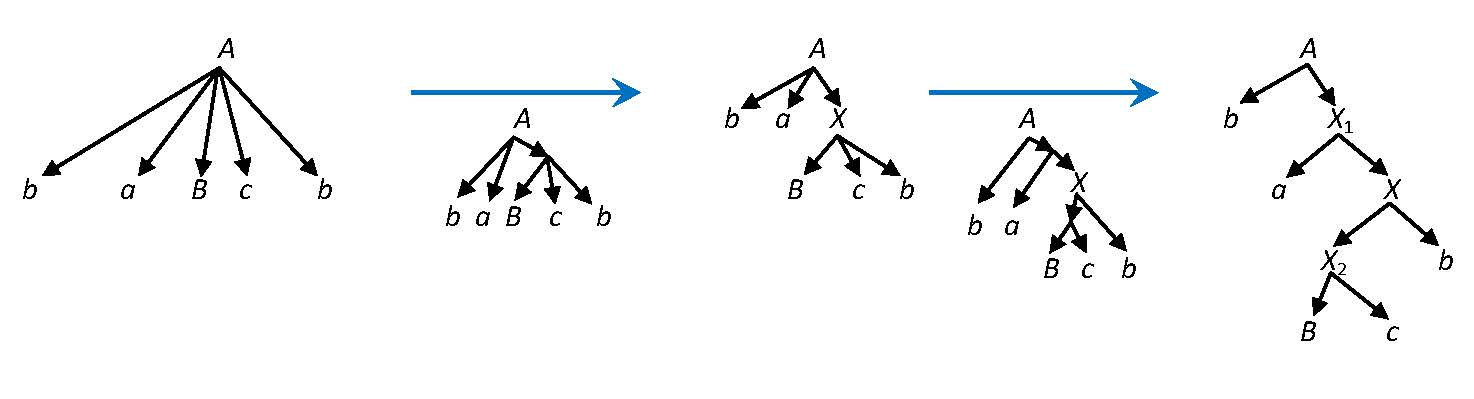 |
Now let us eliminate the rules having more than one terminal in their right hand side (i.e., they have long right hand side). Actually, rules of the form A → a1... ak for k > 1, where ai ∈ T, i ∈ {1,...,k} and A → a1... akB for k > 1, where ai ∈ T, i ∈ {1,...,k}, B ∈ N''' can be substituted in the same manner as we have eliminated them in regular grammars (see the proof of Theorem 2 for details). We present a similar technique for the rules of the form A → Ba1... ak for k > 1, where ai ∈ T, i ∈ {1,...,k}, B ∈ N''', since rules of this type were not present in regular grammars. Every rule of the above form is substituted by a chain of shorter rules introducing new nonterminals into the grammar: let the new nonterminals X1,..., Xk-1 be introduced and put to the set N''', and instead of the actual rule the next set of rules is added to P''':
A → X1ak, X1 → X2ak-1, ..., Xk-2 → Xk-1a2, Xk-1 → Ba1.
(See the right hand side of Figure 3.1, for an example.)
Now a grammar G'''' = (N'''', T, S' ,P'''') is obtained and the set of productions P'''' can contain only rules of the following forms
A → a, A → aB, A → Ba, A → B, S' → λ
(A, B ∈ N'''', a ∈ T). Now, as a final step of our (algorithm) proof we need to exclude the chain rules (rules of the form A → B). This step can be done in a similar way as we showed in the proof of Theorem 2: first the set U(A) is determined for each nonterminal A, and then the grammar G' = (N'''', T, S', P') is obtained having P' = {A → r∣∃ B ∈ N'''' such that B → r ∈ P'''', r ∉ N'''' and B ∈ U(A)}. This grammar is in a normal form and it generates the same language as G, so the (construction) proof is finished.
QED.
Example 37. Let
G = ({S, A, B},{1,3,7}, S,
{ S → 11S37,
S → 7A,
S → B313,
A → 333B7777,
A → S, B → λ, B → 731
}). Give a linear grammar in a normal form that is equivalent to G.
Solution:
Since there is a rule B → λ in the grammar, we start by applying the Empty-word lemma. Then set U = {B} and it is the set of nonterminals from which the empty word λ can be derived. Consequently, we obtain the grammar
G'' = ({S, A, B}, {1,3,7}, S,
{ S → 11S37,
S → 7A,
S → B313, S → 313,
A → 333B7777, A → 3337777,
A → S,
B → 731 \\
}).We have the rules S → 11S37 and A → 333B7777 having terminals on both sides of the nonterminal in the right hand side, thus, the intermediate step results in the grammar
G''' = ({S, A, B, X1, X2}, {1,3,7}, S,
{ S → 11X1, X1 → S37,
S → 7A,
S → B313,
S → 313,
A → 333X2, X2 → B7777,
A → 3337777,
A → S,
B → 731
}).Now let us replace the rules with more than one terminals on their right hand side by chains of rules having exactly one terminal on their right hand sides:
G'''' = ({S, A, B, X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X16, X17, X18, X19, X20, X21}, {1,3,7}, S,
{ S → 1X3, X3 → 1X1,
X1 → X47, X4 → S3,
S → 7A,
S → X53, X5 → X61, X6 → B3,
S → 3X7, X7 → 1X8, X8 → 3,
A → 3X9, X9 → 3X10, X10 → 3X2,
X2 → X117, X11 → X127, X12 → X137, X13 → B7,
A → 3X14, X14 → 3X15, X15 → 3X16, X16 → 7X17, X17 → 7X18, X18 → 7X19, X19 → 7,
A → S,
B → 7X20, X20 → 3X21, X21 → 1
}).However, grammar G'''' contains the chain rule A → S, and thus
U(S) = {S}, U(A) = {A,S},
for the other nonterminals the trivial sets are obtained since they do not appear in any chain rules: U(B) = {B} and U(Xi) = {Xi} (for 1 ≤ i ≤ 21). Thus, the result is:
G' = ({S, A, B, X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11, X12, X13, X14, X15, X16, X17, X18, X19, X20, X21}, {1,3,7}, S,
{ S → 1X3, A → 1X3,
X3 → 1X1,
X1 → X47,
X4 → S3,
S → 7A, A → 7A,
S → X53, A → X53,
X5 → X61,
X6 → B3,
S → 3X7, A → 3X7,
X7 → 1X8,
X8 → 3,
A → 3X9,
X9 → 3X10,
X10 → 3X2,
X2 → X117,
X11 → X127,
X12 → X137,
X13 → B7,
A → 3X14,
X14 → 3X15,
X15 → 3X16,
X16 → 7X17,
X17 → 7X18,
X18 → 7X19,
X19 → 7,
B → 7X20,
X20 → 3X21,
X21 → 1
}).It is linear, in normal form and equivalent to G.
As special cases of linear grammars the right-linear grammars (i.e., our regular grammars) and also the so-called left-linear grammars are defined.
Definition 20. (Left-linear grammars). A grammar G = (N, T, S, P) is left-linear if each of its productions has one of the following forms: A → u, A → Bu, where A,B ∈ N, u ∈ T*.
We state the following interesting result about the languages that can be generated by left-linear grammars, without proof.
Theorem 12. The language class that can be generated by left-linear grammars is exactly the class of regular languages.
We note here that even though regular languages can be generated by using left linear or right linear rules, using both in the same grammar leads to a different language class.
Finally, in this section, we provide a few exercises.
Exercise 49. Give a linear grammar that generates the language
{0m 1n 2n∣n, m ∈ ℕ}.
Exercise 50. Give a linear grammar that generates the language
{a3n b2n∣n,m ∈ ℕ}.
Exercise 51. Give a linear grammar in normal form that generates the language
{ucv∣u, v ∈ {a,b}* such that the number of a's are the same in u and v}.
Exercise 52. Let
G = ({S, A, B, C}, {a, b, c}, S,
{ S → aaSbc,
S → B,
S → cccC,
A → λ,
A → aaa,
A → aCabc,
B → A,
B → Bbbb,
C → cAb,
C → c
}).Give a linear grammar in normal form that is equivalent to G.
It will be shown in the next chapter, that the class of pushdown automata accepts exactly the class of context-free languages (Section 4.6). The class of linear languages can be recognized by a class of special pushdown automata, called one-turn pushdown automata. We will present these automata in detail in Subsection 4.6.4., when we are familiar with the concept of pushdown automata.
In this section we show that the class of linear languages is closed under union, but it is not closed under other regular operations and under other set-theoretical operations.
Theorem 13. The class of linear languages is closed under union, i.e., the union of any two linear languages is also linear.
Proof. The proof is constructive. Let L1 and L2 be linear languages. Let the linear grammars G1 = (N1, T, S1, P1) and G2 = (N2, T, S2, P2) generate the languages L1 and L2 such that N1 ∩ N2 = ∅ (this can be done by renaming nonterminals of a grammar without affecting the generated language). Then, let
G = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1, S → S2}),
where S ∉ N1 ∪ N2, is a new symbol. It can be seen that G generates the language L1 ∪ L2.
QED.
Theorem 14. The class of linear languages is not closed under concatenation and Kleene-star.
Instead of a formal proof we offer a suggestion:
Let us consider the language
L = {anbn∣n > 0}.
The languages L · L and L* are not linear languages.
Theorem 15. The class of linear languages is not closed under complement and intersection.
Proof. Let us start with the intersection. Observe that both of the languages
L1 = {aj bjck∣j, k ∈ ℕ} and L2 = {akbjcj∣j, k ∈ ℕ}
are linear. The intersection of these two languages is
L = L1 ∩ L2 = {ajbjcj∣j ∈ ℕ}.
As we will prove it in Example this language is not context-free, and therefore it is not linear. This proves the non closure under intersection.
We are going to prove now that the class is not closed under complement. Consider the following language: {wcw∣w ∈ {a,b}*} over the alphabet {a,b,c}. It is called the language of ''marked-copy''. In Example 43. we prove that this language is not context-free, and thus it is not linear. However, the complement of this language is a linear language.
QED.
Exercise 53. Give a linear grammar that generates the complement of the language of marked-copy. Hints: it can be done as union of linear languages. A word can be in this complement if,
it does not contain any c,
it does contain at least two c's,
it is of the form u c v, with u,v ∈ {a,b}*, but ∣u∣≠∣v∣,
it is of the form u c v, with u,v ∈ {a,b}*, and ∣u∣=∣v∣, but there is a mismatch letter: u = u1xu2 and v = u1yu2, where x,y ∈ {a,b}, but x ≠ y.
Exercise 54. Give a grammar that generates the union of the languages generated by grammars G1 and G2, where
G1 = ({S1, A1, B1}, {a,b,c}, S1,
{ S1 → aaS1ccc,
S1 → A1,
A1 → bB1b,
B1 → bB1,
B1 → b
})and
G2 = ({S2, A2, B2, C2}, {a,b,c}, S2,
{ S2 → cccS2aa,
S2 → bA2,
A2 → A2b,
A2 → cB2aa,
A2 → C2,
B2 → bB2,
B2 → baccab,
C2 → C2c,
C2 → A2
}).Table of Contents
Summary of the chapter: This chapter will mainly deal with the properties of the type-2 language class of the Chomsky hierarchy, called context-free languages. This language class has many practical applications used in various areas of computer science. We will mention some of the most important ones. First, we discuss the notation techniques used to describe the syntax of programming languages, the Backus-Naur form, and the syntax diagram. Second, we introduce a normal form for context-free languages. This normal form will be used in Section 4.5., which is dedicated to parsing. The first pumping lemma, the Bar-Hillel lemma will be explained, and the closure properties of the context-free language class will be proven. In the last part of this chapter we introduce the pushdown automaton, we show its features, and its applications.
Notation techniques were introduced as simple methods to describe different parts of programming languages. These parts contain terminal and nonterminal symbols. Terminals are given, and nonterminals can be built up from terminals and already defined nonterminals by using simple operations. These operations are the following:
Concatenation, when symbols are written after each other.
Alternation is a selection from different possibilities.
Option is a special selection between a symbol and the empty word.
Repetition, when a symbol can be repeated any (≥ 0) number of times.
In this section we introduce two well known techniques, the Backus-Naur form (BNF) and the Syntax diagram, but many others have been introduced for a variety of reasons. For example, the Extended Backus-Naur form is an extended version of the standard BNF.
BNF was designed by Peter Naur in 1963 as a simplified version of the notation technique of John Backus. It was used first to describe the programming language ALGOL60. Table 4.1. shows the marking of the operations used by BNF.
Table 4.1. Operations of the BNF metasyntax.
| Definition | Concatenation | Alternation | Option | Repetition |
|---|---|---|---|---|
| ∷= | ∣ | [] | {} |
As you can see, concatenation does not have any special mark, we just write the symbols after each other. We use a terminal symbol as it is, for example, the mark of one as a number is 1. For nonterminals we use their names between angle brackets. We have a special mark to define nonterminal symbols, followed by the description of the nonterminal.
Example 38. In this example, we describe a non-negative binary number using BNF metasyntax.
< digit > ::= 0 ∣ 1
< positive > ::= [ + ] 1 { < digit > }
< number > ::= 0 ∣ < positive >
A syntax diagram is a graphical notation technique. It uses simple graphs, each of them has an entry and an end point. The concatenation, alternation, option and repetition operations are implemented in the structure of the graph.
Example 39. Figure 4.1. describes a non-negative binary number using the syntax diagram.
A generative grammar is said to be λ-free grammar if none of its production rules contains the empty word λ on the right hand side. We have to note that each λ ∉ L context-free language can be generated by some λ-free context-free grammar.
Definition 21. The grammar G = (N, T, S, P) is in Chomsky normal form, if all of its production rules has the form:
A → BC or
A → a,
where A, B, C ∈ N and a ∈ T.
This normal form was introduced by Noam Chomsky for λ-free context-free languages. Using the Chomsky normal form instead of the universal context-free grammar makes it more simple to store the grammar in the memory of the computer, to calculate using the grammar and to prove theorems about context-free languages. First, we have to prove that each λ-free context-free language can be generated by a Chomsky normal form grammar.
Theorem 16. For each λ-free context-free grammar G = (N, T, S, P) one can give Chomsky normal form grammar G' = (N', T, S, P') such that L(G) = L(G').
Proof. We are going to give a constructive proof of this theorem. We are going to show the necessary steps to construct a Chomsky normal form grammar G' = (N', T, S, P') which is equivalent to the original λ-free context-free grammar G = (N, T, S, P). It can easily be seen that we get equivalent grammars after each step.
First of all we create the grammar G1 = (N1, T, S, P1) such that all of its production rules are of the form:
A → p, or
A → a,
where A ∈ N, a ∈ T and p ∈ N+. In this step we eliminate each terminal symbol from the production rules whose right-hand side contains more than one letter. To do this we introduce new nonterminal symbols for each such terminal symbol. Let the set of new nonterminals be Nnew = {X∣a ∈ T, A → paq ∈ P, ∣pq∣≠ 0} and let N1 = N ∪ Nnew. Then let the set P1 be the union of 3 different sets:
{A → p∣A → p ∈ P, p ∈ {T ∪ N+}} ⊂ P1 (we keep the rules for which the right hand side contains just one terminal, or contains only nonterminal symbols),
{X → a∣X ∈ Nnew} ⊂ P1 (we add new rules, the right hand side contains the terminal symbol, and the left hand side contains the nonterminal introduced for it),
{A → p0X1p1X2... Xnpn∣A → p0a1p1a2... anpn ∈ P, a1, a2,...,an ∈ T, X1, X2,...,Xn ∈ Nnew, p0, p1,...,pn ∈ N*, ∣p0a1p1a2... anpn∣≥ 2} ∈ P1 (here we change each appearance of the terminals to the nonterminal introduced for it in each rule, with right hand side of at least two letters).
Now we have the sets N1 and P1 and the grammar G1 = (N1, T,S,P1) satisfies the above conditions. It can be easily shown that L(G1) = L(G).
The next step is to eliminate the long rules. We create the grammar G2 = (N2, T, S, P2) such that all of its production rules are of the form:
A → B, or
A → BC, or
A → a,
where A, B, C ∈ N and a ∈ T. To reach our goal, we have to replace the long rules in P1 with short ones in P2. For each rule A → B1B2...Bk ∈ P1, k ≥ 3 we introduce new nonterminals Z1, Z2,...,Zk-2. The set N2 contains these new nonterminals and the nonterminals contained by the set N1. In the set P2 we keep those productions rules from the set P1 whose right hand side contains at most two letters and instead of each A → B1B2...Bk ∈ P1, k ≥ 3 rule we introduce the rules
A → B1Z1, Z1 → B2Z2, ⋮ Zk-3 → Bk-2Zk-2, Zk-2 → Bk-1Bk.
The grammar G2 = (N2, T, S, P2) has no long rules and L(G2) = L(G1).
The third step is to eliminate the rules of the form A → B, where A, B ∈ N.
First, for each nonterminal letter A let us collect all nonterminal letters B1, B2, ..., Bk such that A can be derived from Bi, 1 ≤ i ≤ k. Let U(A) = {B1, B2, ..., Bk} for each nonterminal A. The following formulas make this pocedure simple:
U1(A) = {A}
Ui+1(A) = Ui(A) ∪ {B∣B → C ∈ P2, C ∈ Ui(A)}
if Uk(A) = Uk+1(A) then U(A) = Uk(A)
When we have set U for each nonterminal letter, we can define set P' with the following formula: P' = {B → p∣A → p ∈ P2, B ∈ U(A), p ∉ N2}. Then N' = N2, G' = (N', T, S, P') and L(G') = L(G2) = L(G1) = L(G).
QED.
Example 40. In this example we have a λ-free context-free grammar G, and we are going to create the grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S, A, B}, {a,b,c},S, P) P = { S → ABaba, A → c, A → B, A → AS, B → AbA, B → S }
The terminals a and b appear in a rule which has more than 1 letter on the right hand side, so we have to add two new nonterminals Xa and Xb to the set of nonterminals: N1 = {S, A, B, Xa, Xb}. Now we add two new rules (Xa → a and Xb → b) to the set of production rules and replace the terminal symbol a by Xa and b by Xb in the rules which have more than one letter on the right hand side. Now we have
G1 = ({S, A, B, Xa, Xb}, {a,b,c}, S, P1), P1 = { A → c, A → B, A → AS, B → S, Xa → a, Xb → b, S → ABXaXbXa, B → AXbA }.
In the set P1 there are two long rules, S → ABXaXbXa and B → AXbA. We add new nonterminals Z1, Z2, Z3 to the first rule and Z4 to the second one, and replace the rule S → ABXaXbXa by rules
S → AZ1, Z1 → BZ2, Z2 → XaZ3, Z3 → XbXa, and the rule B → AXbA by rules B → AZ4, Z4 → XbA. Now we have G2 = ({S, A, B, C, D, Z1, Z2, Z3, Z4}, {a,b,c}, S, P2), P2 = { A → c, A → B, A → AS, B → S, Xa → a, Xb → b, S → AZ1, Z1 → BZ2, Z2 → XaZ3, Z3 → XbXa, B → AZ4, Z4 → XbA }.
U(B) = {B,A} and U(S) = {S,B,A}, and finally we have:
G' = ({S, A, B, C, D, Z1, Z2, Z3, Z4}, {a,b,c}, S, P'). P' = { A → c, A → AS, Xa → a, Xb → b, S→ AZ1, B → AZ1, A → AZ1, Z1 → BZ2, Z2 → XaZ3, Z3 → XbXa, B → AZ4, A → AZ4, Z4 → XbA }
Exercise 55. In this exercise we have a λ-free context-free grammar G, and you have to create a grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S, A, B}, {x,y,z}, S, P) P = { S → BB, A → S, A → xxzz, A → y, B → AxzxA, B → A }
Exercise 56. Create a grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S, A, B}, {x,y}, S, P) P = { S → ABBAB, S → x, A → BB, A → S, A → B, B → ASA, B → y }
Exercise 57. Create a grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S, X, Z}, {x,y}, S, P) P = { S → XZ, S → ZX, X → xy, X → S, Z → S, Z → yx, Z → X, Z → ZZ }
Exercise 58. Create a grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S}, {a,+,*,(,)}, S, P) P = { S → S+S, S → S*S, S → (S), S → a }
Exercise 59. Create a grammar G' which is in Chomsky normal form and generates the same language as G.
G = ({S, A, B}, {x,y}, S, P) P = { S → AxxB, S → A, S → B, B → A, A → y, A → SB }
Although it is easy to find the exact position of a grammar in the Chomsky hierarchy, it is sometimes much more challenging to find the position of a language in the Chomsky hierarchy. The Bar-Hillel lemma is the first pumping - also called iteration - lemma, which gives properties shared by all context-free languages. Thus, if a language does not satisfy the conditions of the lemma, it is not context-free. This lemma - and its variations - can be used to show that a language is not context-free. On the other hand, languages satisfying the conditions may be not context-free.
Theorem 17. (Bar-Hillel lemma) For each context-free language L there exists an integer n ≥ 1 such that each string p ∈ L, ∣p∣ ≥ n can be written in a form p = uvwxy, where ∣vwx∣ ≤ n, ∣vx∣ ≥ 1 and uviwxiy ∈ L holds for each integer i ≥ 0.
Proof. Let L1 = L \ {λ}. It is ovious that if language L1 satisfies the above conditions then language L = L1 ∪ {λ} also holds the above conditions, so it is enough to prove the lemma for λ-free context-free languages.
Theorem 16 shows that each λ-free context-free language can be generated by a Chomsky normal form grammar. Further on let us assume that grammar G generating L1 is in Chomsky normal form.
Let us mark the number of nonterminals in grammar G by k, and let n = 2k+1. Let p be a word generated by grammar G, and let ∣p∣ ≥ n. In this case, the height of the derivation tree of p is more than k+2, where the last step is a nonterminal to terminal derivation. Let us investigate the last k+2 height part of the longest path of the derivation tree. There must be a nonterminal A which appears twice, because the number of the nonterminals in G is less than the number of the nonterminals in this part. So there must be terminal words v, x such that A ⇒* vAx. Here ∣vx∣ ≥1 because A has two different occurrences in the path, and the length of the generated word is increased by one in each derivation step, except for the derivation steps when we change a nonterminal to a terminal symbol. Also, there is a terminal word w, which can be derived from the last appearance of A on the path, so A ⇒* w also holds. Moreover, there are terminal words u, y such that S ⇒* uAy. Based on these facts it is easy to show that
S ⇒* uAy ⇒* uwy S ⇒* uAy ⇒* uvAxy ⇒* uvwxy S ⇒* uAy ⇒* uvAxy ⇒* uvvAxxy ⇒* uvvwxxy ⋮
This proves that uviwxiy ∈ L holds for each integer i ≥ 0.
Finally, ∣vwx∣ ≤ n, because the word vwx was derived with a derivation subtree of height at most k+2, - where the last step was a nonterminal to terminal derivation, - so the length of the word vwx is maximum 2k which is less than n.
QED.
Example 41. The following classical example shows an application of the Bar-Hillel lemma. We are going to prove that language L = {ajbjcj∣j ≥ 0} is not context-free. In order to do this suppose to the contrary that language L is context-free. Let j ≥ (n / 3), then, by the Bar-Hillel lemma, ajbjcj can be written in a form uviwxiy such that ∣vx∣ ≥ 1 and uviwxiy ∈ L holds for each integer i ≥ 0. First, neither of v nor x should contain two or more different letters, because repeating them would change the form of the words in L. So v is a unary word (some power of a letter, e.g. aa...a) and x is a unary word as well. In this case, when we increase the integer i, we change the number of one or two different letters, but we cannot change the number of each letter, which is a contradiction.
Example 42. Let us consider the language L ={ajbkcjdk∣j, k ≥ 0}. Suppose to the contrary that language L is context-free. Then, the word anbncndn ∈ L can be written in a form uvwxy such that uviwxiy ∈ L for each i ≥ 0. Suppose that the word v contains the letter a. In this case, the word x cannot contain the letter c, because ∣vwx∣ ≤ n. Also, if the word v contains the letter b, then the word x cannot contain the letter d. In this case, we cannot increase the number of the letters a and c at the same time, and also we cannot increase the number of the letters b and d together, which means that this language does not satisfy the conditions of the Bar-Hillel lemma, consequently it is not context-free.
Example 43. In this example we consider the language L = {wcw∣w ∈ {a,b}*}, and we use the Bar-Hillel lemma to prove that this language is not context-free. Suppose to the contrary that the language L is context-free, in this case the word anbncanbn can be written in a form uvwxy such that uviwxiy ∈ L for each i ≥0. The only possible solution is that the word v contains letters before the letter c and the word x contains letters after the letter c, because in other cases the number of the letters before and after c will not be the same. Now, ∣vwx∣≤ n, so the word v can contain only letter b and the word x can contain only letter a, which is a contradiction.
Example 44. In this example we show that the language L = {ap∣p pime} is not context-free. Suppose to the contrary that the language L is context-free. Let p ≥ n, so ap can be written in a form uvwxy such that ∣vx∣ ≥ 1 and uviwxiy∈ L holds for each integer i ≥ 0. Now, let q = ∣vx∣, r = ∣uwy∣, so ar+i · q∈ L holds for each integer i ≥ 0. This means that r+i · q is a prime for each integer i ≥ 0. Here r ≠ 1, because 1+i · q = 1 for i = 0, and 1 is not a prime number. Let i=r, then r+r · q should be a prime, but r+r · q = r · (1+q) is not a prime, so we have a contradiction.
Theorem 18. The context-free language class is closed under regular operations.
Proof. We are going to give a constructive proof for each regular operation one by one. We use two context-free languages, L1 and L2. Let the grammar G1 = (N1, T, S1, P1) such that L(G1) = L1, and let the grammar G2 = (N2, T, S2, P2) such that L(G2) = L2. Without loss of generality we can suppose that N1 ∩ N2 = ∅. We are going to give the context-free grammars GUn, GCo and GKl, such that L(GUn) = L1 ∪ L2, L(GCo) = L1 · L2 and L(GKl) = L1*.
Union
To create the grammar GUn we need a new start symbol S, such that S ∩ N1 = S ∩ N2 = S ∩ T = ∅. Then, let
GUn = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1, S → S2}).
Concatenation
For the grammar GCo we also need a new start symbol S, such that S ∩ N1 = S ∩ N2 = S ∩ T = ∅. Then, let
GCo = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1S2}).
Kleene star
For the grammar GKl we again use a new start symbol S, where S ∩ N1 = S ∩ T = ∅. Then, let
GKl = (N1 ∪ {S}, T, S, P1 ∪ {S → λ, S → SS1}).
QED.
Theorem 19. The context-free language class is not closed under intersection.
Proof. It is easy to prove this theorem, because we need only one counterexample. Let the language L1 = {aibicj∣i, j ≥ 0}. L1 is context-free, because we have a context-free grammar G1 = ({S, A}, {a,b,c}, S, {S → Sc, S → A, A → aAb, A → λ}) such that L1 = L(G1). Let the language L2 = {aibjcj∣i, j ≥ 0}. The language L2 is also context-free, because we have a context-free grammar G2 = ({S, A}, {a,b,c}, S, {S → aS, S → A, A → bAc, A → λ}) such that L2 = L(G2). The intersection of these two languages is L1 ∩ L2 = {ajbjcj∣j ≥ 0}, and in the example 41 it is proven by the Bar-Hillel lemma that this language is not context-free.
QED.
Theorem 20. The context-free language class is not closed under the complement operation.
Proof. Now we use proof by contradiction. The set theoretical version of one of the well known De Morgan's laws says
that 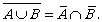 With a slight modification, we have
With a slight modification, we have 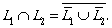 Suppose to the contrary that the context-free languages are closed under the complement operation.
In this case, if L1 and L2 are context-free languages,
the language defined by the right hand side of the expression must be context-free,
however, since the left hand side may be non-context-free as in the previous theorem, a contradiction.
Suppose to the contrary that the context-free languages are closed under the complement operation.
In this case, if L1 and L2 are context-free languages,
the language defined by the right hand side of the expression must be context-free,
however, since the left hand side may be non-context-free as in the previous theorem, a contradiction.
QED.
Theorem 21. The intersection of a context-free language and a regular language is always context-free.
Proof. We are going to give a constructive proof for this theorem. Let L1 be a context-free language, and let L2 be a regular language, where L2 = L21 ∪ L22 ∪...∪ L2n, and where each L2i(1 ≤ i ≤ n) is accepted by a deterministic finite automaton which has only one final state. We can do it without loss of generality, because it is well established fact that each regular language can be written in this form. Now
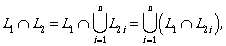
because intersection distributes over union. Since context-free languages are closed under union, we only have to show that L1 ∩ L2i is context-free for each i. Let the grammar G = (N, T, S, P) be a Chomsky normal form grammar such that L(G) = L1 \ {λ}, and let DFAi = (Q, T, q0, δ, qf) be a deterministic finite automaton such that L(DFAi) = L2i. Now, we are going to define the context-free grammar G' = (N', T, S', P') such that L(G') = L1 ∩ L2i. The set of the nonterminals of G' is N' = {A[q1,B,q2]∣ for each q1, q2 ∈ Q, B ∈ N}. The production rules of the grammar G' are the following:
S' → A[q0,S,qf] ∈ P',
A[q1,B,q3] → A[q1,C,q2] A[q2,D,q3] ∈ P' for each possible q1, q2, q3 ∈ Q, if B → CD ∈ P,
A[q1,B,q2] → a ∈ P' if B → a ∈ P and δ(q1,a) = q2,
S' → λ ∈ P', if λ ∈ L1 and q0 = qf.
It is easy to see that the grammar G' generates the word p, if and only if it is generated by grammar G, and it is accepted by the automaton L2i as well. Each production rule of the grammar G' is context-free, so the language generated by the grammar G' is context-free.
QED.
In formal language theory, parsing - or the so called syntactic analysis - is a process when the parser determines if a given string can be generated by a given grammar. This is very important for compilers and interpreters. For example, it is not too difficult to create a context-free grammar GP generating all syntactically correct Pascal programs. Then, we can use a parser to decide - about a Pascal program written by a programmer - if the program is in the generated language L(GP). When the program is in the generated language, it is syntactically correct.
We have a given Chomsky normal form grammar G = (N, T, S, P) and a word p = a1a2... an. The Cocke-Younger-Kasami algorithm is a well known method to decide wether p ∈ L(G) or p ∉ L(G). To make our decision, we have to fill out an n × n size triangular matrix M in the following way: Over the cells of the first line, we write the letters a1,a2,...,an, starting from the first letter, one after the other. Then, the cell M(i,j) contains each nonterminal symbol A, if and only if the subword ajaj+1...aj+i-1 can be derived from A. (Formally: A ∈ M(i,j) if and only if A →* ajaj+1...aj+i-1.) This means that the first cell of the first line contains the nonterminal A, if and only if A → a1 ∈ P. The cell M(1,j) contains the nonterminal A, if and only if A → aj ∈ P. It is also quite easy to fill out the cells of the second line of the matrix. The nonterminal A is in the cell M(2,j), if and only if there exists nonterminals B, C ∈ N such that B ∈ M(1,j), C ∈ M(1,j+1), and A → BC ∈ P. From this point the algorithm becomes more complex. From the third line, we use the following formula: A ∈ M(i,j), if and only if there exists nonterminals B, C ∈ N and integer k such that B ∈ M(k,j), C ∈ M(i-k, j+k) and A → BC ∈ P. This algorithm is finished when the cell M(n,1) is filled out. Remember, the nonterminal A is in the cell M(i,j), if and only if the word ajaj+1...aj+i-1 can be derived from A. This means that the nonterminal S is in the cell M(n,1), if and only if the word a1a2...an can be derived from S. So the grammar G generates the word p, if and only if the cell M(n,1) contains the start symbol S.
Example 45. In this example, we use the CYK algorithm to show that the grammar G generates the word abbaa.
G = ({S, A, B}, {a,b}, S, P) P = { S → SA, S → AB, A → BS, B → SA, S → a, A → a, B → b }
As you can see, S ∈ M(5,1), so abbaa ∈ L(G).
Exercise 60. Use the CYK algorithm to show that the grammar G generates the word baabba.
G = ({S, A, B, X, Y, Z}, {a,b}, S, P) P ={ S → AY, Y → XB, X → BA, X → ZA, Z → BX, A → b, B → a }
Exercise 61. Use the CYK algorithm to decide if the word cbacab can be generated by grammar G.
G = (S, A, B, C, D}, {a,b,c}, S, P) P = { S → AB, A → CA, A → SS, B → CD, A → b, C → a, C → b, D → c }
The Earley algorithm is designed to decide if a context-free grammar generates a terminal word. Sometimes it is not comfortable to create and use an equivalent Chomsky normal form grammar for a λ-free context-free grammar, because the Chomsky normal form grammar could have many more production rules than the original grammar. This is why the Earley algorithm is more widely used than the CYK algorithm for computerized lexical analysis. Although the Earley algorithm looks more complicated for humans, - and actually, it is more complicated compared to the the very simple CYK algorithm, - but after the implementation, there is no difference between the complexity of the two algorithms for computers.
Now we are going to show the steps of the λ-free version of the Earley algorithm. It can work with rules having form A → λ as well, with minor modification, but in practice we do not need the extended version.
Let G = (N, T, S, P) be a λ-free, context-free grammar, and p = a1a2... an ∈ T+, with integer n > 0. We are going to fill out the cells of an (n+1) × (n+1) triangular matrix M, except for the last cell M(n,n). Over the cells of the first line of the matrix, we write the letters a1, a2,..., an, starting from the second cell and first letter, one after the other. The elements of the matrix are production rules from P, where the right hand side of each rule contains a dot character.
The steps of the algorithm are the following:
Let S → .q ∈ M(0,0) if S → q ∈ P, and let j = 0.
Let A → .q ∈ M(j,j) if A → q ∈ P, and there exists an integer k≤ j such that B → r.At ∈ M(k,j).
Let j = j+1 and let i = j-1.
Let A → raj.t ∈ M(i,j) if A → r.ajt ∈ M(i,j-1).
Let A → rB.t ∈ M(i,j) if there exists an integer i ≤ k < j such that A → r.Bt ∈ M(i,k), and B → q. ∈ M(k,j).
If i > 0 then i = i-1 and goto 4.
If i = 0 and j < n then goto 2.
If i = 0 and j = n then finished.
Here q ∈ (T ∪ N)+, A, B ∈ N, r, t ∈ (T ∪ N)*, and of course i,j,k are integers.
Grammar G generates the word p (p ∈ L(G)), if and only if there is a production rule in M(0,n), whose left hand side is the start symbol S, and there is a dot at the end of the right hand side of the rule.
Examplee 46. In this example, we have a λ-free context-free grammar G, and we have to decide if the word a*a+a can be generated by this grammar.
G = ({S, A, B}, {a,+,*,(,)}, S, P) P = { S → S+A A → A*B B → (S) S → A A → B B → a }
As you can see, the top right cell contains a rule, whose left hand side is the start symbol S, and there is a dot at the end of the right hand side of the rule, so a+a*a ∈ L(G).
Exercise 62. Use the Earley algorithm to decide if the word 100110 can be generated by grammar G.
G = ({S, A, B}, {0,1}, S, P) P = { S → 0A1, S → 1B0, A → B1, B → S1, A → 0, B → 1 }
Exercise 63. Use the Earley algorithm to decide if the word bbabb can be generated by grammar G.
G = ({S, A, B}, {a,b}, S, P) P = { S → BA B → bAB, A → BAb, B → SbA, A → a, B → b }
Finite automata can accept regular languages, so we have to extend its definition so as it could accept context-free languages. The solution for this problem is to add a stack memory to a finite automaton, and the name of this solution is "pushdown automaton". The formal definition is the following:
Definition 22. A pushdown automaton (PDA) is the following 7-tuple:
PDA = (Q, T, Z, q0, z0, δ, F)
where
Q is the finite nonempty set of the states,
T is the set of the input letters (finite nonempty alphabet),
Z is the set of the stack symbols (finite nonempty alphabet),
q0 is the initial state, q0 ∈ Q,
z0 is the initial stack symbol, z0 ∈ Z,
δ is the transition function having a form Q × {T ∪ {λ}} × Z → 2Q×Z*, and
F is the set of the final states, F ⊆ Q.
In order to understand the operating principle of the pushdown automaton, we have to understand the operations of finite automata and the stack memory. Finite automata were introduced in Chapter 2, and we studied them through many pages. The stack is a LIFO (last in first out) memory, which has two operations, PUSH and POP. When we use the POP operation, we read the top letter of the stack, and at the same time we delete it. When we use the PUSH operation, we add a word to the top of the stack.
The pushdown automaton accepts words over the alphabet T. At the beginning the PDA is in state q0, we can read the first letter of the input word, and the stack contains only z0. In each step, we use the transition function to change the state and the stack of the PDA. The PDA accepts the input word, if and only if it can read the whole word, and it is in a final state when the end of the input word is reached.
More formally, in each step, the pushdown automaton has a configuration - also called instantaneous description - (q,v,w), where q ∈ Q is the current state, v ∈ T* is the unread part of the input word, and w ∈ Z* is the whole word contained by the stack. At the beginning, the pushdown automaton is in its initial configuration: (q0, p, z0), where p is the whole input word. In each step, the pushdown automaton changes its configuration, while using the transition function. There are two different kinds of steps, the first is the standard, the second is the so called λ-step.
The standard step is when the PDA reads its current state, current input letter, the top stack symbol, it finds an appropriate transition rule, it changes its state, it moves to the next input letter and changes the top symbol of the stack to the appropriate word. Formally, we can say the PDA can change its configuration from (q1, av, zw) to (q2, v, rw) in one step, if it has a transition rule (q2, r) ∈ δ (q1, a, z), where q1, q2 ∈ Q, a ∈ T, z ∈ Z, v ∈ T*, w ∈ Z*. Denote this transition (q1, av, zw) ⊦PDA (q2, v, rw).
The λ-step is when the PDA reads its current state, it does not read any input letters, it reads the top stack symbol, it finds an appropriate transition rule, and it changes its state, it does not move to the next input letter and it changes the top letter of the stack to the given word. Formally, we can say again that the PDA can change its configuration from (q1, v, zw) to (q2, v, rw) in one step, if it has a transition rule (q2, r) ∈ δ (q1, λ, z), where q1, q2 ∈ Q, z ∈ Z, v ∈ T*, and w ∈ Z*. Mark: (q1, v, zw) ⊦PDA (q2, v, rw).
We can say that the PDA can change its configuration from (q1, v, w) to (q2, x, y) in finite many steps, if there are configurations C0, C1,..., Cn such that C0 = (q1, v, w), Cn = (q2, x, y), and Ci ⊦PDA Ci+1 holds for each integer 0 ≤ i < n. Mark: (q1, v, w) ⊦*PDA (q2, x, y).
Finally, we can define the language accepted by the pushdown automaton:
L(PDA) = {p∣p ∈ T*, (q0, p, z0) ⊦*PDA (qf, λ, y), qf ∈ F, y ∈ Z*}.
Example 47. This simple example shows the description of a pushdown automaton which accepts the language L = {aibicjdj∣i, j ≥ 1}.
PDA = ({q0,q1,q2,q3,q4,q5},{a,b,c,d},{x,z0},q0,z0,δ,{q5}), δ(q0,a,z0) = {(q1,xz0)}, δ(q1,a,x) = {(q1,xx)}, δ(q1,b,x) = {(q2,λ)}, δ(q2,b,x) = {(q2,λ)}, δ(q2,c,z0) = {(q3,xz0)}, δ(q3,c,x) = {(q3,xx)}, δ(q3,d,x) = {(q4,λ}, δ(q4,d,x) = {(q4,λ)}, δ(q4,λ,z0) = {(q5,z0)}.
The Figure 4.6. shows the graphical notation of this pushdown automaton.
Example 48. This example shows the description of a pushdown automaton which accepts the language of words over the alphabet {a,b} containing more a's than b's.
PDA = ({q0,qa,qb},{a,b},{1,z0},q0,z0,δ,{qa}), δ(q0,a,z0) = {(qa,z0)}, δ(q0,b,z0) = {(qb,z0)}, δ(qa,a,z0) = {(qa,1z0)}, δ(qa,a,1) = {(qa,11)}, δ(qa,b,1) = {(qa,λ)}, δ(qa,b,z0) = {(q0,z0)}, δ(qb,b,z0) = {(qb,1z0)}, δ(qb,b,1) = {(qb,11)}, δ(qb,a,1) = {(qb,λ)}, δ(qb,a,z0) = {(q0,z0)}.
The Figure 4.7. shows the graphical notation of this pushdown automaton.
Exercise 64. Create a pushdown automaton, which accepts the language L = {aibj∣0 ≤ i ≤ j ≤ 2i}.
Exercise 65. Create a pushdown automaton, which accepts the language L = {aibjck∣i = j or j = k}.
Exercise 66. Create a pushdown automaton, which accepts the language L = {aibjck∣i = j or i = k}.
There is another method for accepting words with a pushdown automaton. It is called "acceptance by empty stack". In this case, the automaton does not have any final states, and the word is accepted by the pushdown automaton if and only if it can read the whole word and the stack is empty when the end of the input word is reached. More formally, the language accepted by automaton
PDAe = (Q, T, Z, q0, z0, δ)
by empty stack is
L(PDAe) = {p∣p∈T*,(q0,p,z0)⊦*PDAe(q,λ,λ),q∈Q}.
Example 49. This example shows the description of a pushdown automaton which accepts by empty stack the language L = {aibicjdj∣i, j ≥ 1}.
PDA = ({q0,q1,q2,q3,q4,q5},{a,b,c,d},{x,z0},q0,z0,δ,{q5}), δ(q0,a,z0) = {(q1,xz0)}, δ(q1,a,x) = {(q1,xx)}, δ(q1,b,x) = {(q2,λ)}, δ(q2,b,x) = {(q2,λ)}, δ(q2,c,z0) = {(q3,xz0)}, δ(q3,c,x) = {(q3,xx)}, δ(q3,d,x) = {(q4,λ}, δ(q4,d,x) = {(q4,λ)}, δ(q4,λ,z0) = {(q4,λ}.
The Figure 4.8. shows the graphical notation of this pushdown automaton.
Example 50. In this example, we are going to show the description of a pushdown automaton which accepts by empty stack the language with words over the alphabet {a,b} containing the same number of a's and b's.
PDA = ({q0},{a,b},{0,1,z0},q0,z0,δ), δ(q0,a,z0) = {(q0,0z0)}, δ(q0,b,z0) = {(q0,1z0)}, δ(q0,a,0) = {(q0,00)}, δ(q0,b,0) = {(q0,λ)}, δ(q0,b,1) = {(q0,11)}, δ(q0,a,1) = {(q0,λ)}, δ(q0,λ,z0)={(q0,λ)}.
The Figure 4.9. shows the graphical notation of this pushdown automaton.
The language class accepted by pushdown automata by final states and the language class accepted by pushdown automata by empty stack are the same. To prove this, we use two lemmas. First, we prove that for each PDA we can give PDAe such that L(PDAe) = L(PDA), second we show the reverse case.
Lemma 1. For each PDA = (Q, T, Z, q0, z0, δ, F) we can give PDAe = (Q', T, Z, q0, z0,δ') such that L (PDAe) = L(PDA).
Proof. We are going to define a pushdown automaton PDAe, which works the same way as the pushdown automaton PDA does, but each time when the original automaton goes into a final state, the new automaton goes into the state qf, as well. Then, PDAe clears out the stack, when it is in the state qf. Formally, let Q' = Q ∪ {qf} where {qf} ∩ Q = ∅, and the transition function is the following:
Let (q2,r) ∈ δ' (q1,a,z) if (q2,r) ∈ δ (q1,a,z), for each q1, q2 ∈ Q, a ∈ T ∪ {λ}, z ∈ Z, r ∈ Z*,
let (qf,λ) ∈ δ' (q1,a,z) if (q2,r) ∈ δ (q1,a,z), for each q1 ∈ Q, q2 ∈ F,a ∈ T ∪ {λ}, z ∈ Z,r ∈ Z*, and
let δ' (qf,λ,z) = {(qf,λ)} for each z ∈ Z.
QED.
Lemma 2. For each PDAe = (Q, T, Z, q0, z0, δ) we can give PDA = (Q', T, Z', q'0, z'0, δ', F) such that L(PDA) = L(PDAe).
Proof. Again, we have a constructive proof. The automaton PDA first puts the initial stack symbol of the automaton PDAe over the new initial stack symbol. Then it simulates the original PDAe automaton, but each time when the original automaton clears the stack completely, the new automaton goes into the new final state qf. The automaton PDA defined below accepts the same language with final states which is accepted by the original automaton PDAe with empty stack. Let Q' = Q ∪ {q'0,qf}, where {q'0} ∩ Q = {qf} ∩ Q = ∅, let Z' = Z ∪ {z'0}, where {z'0} ∩ Z = ∅, and let F = {qf}, so {qf} is the only final state, q'0 is the new initial state, and z'0 is the new initial stack symbol. The transition function is the following:
Let δ'(q'0, λ, z'0) = {(q0,z0z'0)},
let (q2,r) ∈ δ' (q1,a,z) if (q2,r) ∈ δ (q1,a,z), for each q1, q2 ∈ Q, a ∈ T ∪ {λ}, z ∈ Z, r ∈ Z*, and
let δ'(q,λ,z'0) = {(qf,λ)} for each q ∈ Q.
QED.
Theorem 22. The language class accepted by pushdown automata with final states is the same as the language class accepted by pushdown automata with empty stack.
Proof. This theorem is a direct consequence of Lemma 1. and Lemma 2.
QED.
The proof of Lemma 2. has the following consequences:
For each pushdown automaton we can give another pushdown automaton which accepts the same language with only one final state.
For each pushdown automaton we can give another pushdown automaton which accepts the same language with a final state and with empty stack at the same time.
In this subsection we are going to prove that the languages accepted by pushdown automata are the context-free languages. Again, we are going to give constructive proofs. First, we demonstrate that for each pushdown automaton we can give a context-free grammar generating the same language as accepted by the PDAe with empty stack, then we show how to construct a PDAe which accepts the language generated by a context-free grammar.
Lemma 3. For each PDAe = (Q, T, Z, q0, z0, δ) we can give a context-free grammar G = (N, T, S, P) such that L(G) = L(PDAe).
Proof. The set of input letters of the PDAe and the set of terminal symbols of grammar G are the same. The set of nonterminal letters is N = {S} ∪ {A[q,z,t]∣ for each q, t ∈ Q, z ∈ Z}. The production rules are the following:
S → A[q0,z0,q] ∈ P for each q ∈ Q,
A[q,z,t] → aA[t,z1,q1] A[q1,z2,q2]... A[qn-1,zn,qn] ∈ P for each possible q1,..., qn ∈ Q, if (t, z1z2... zn) ∈ δ (q,a,z), where a ∈ T ∪ {λ},
A[q,z,t] → a ∈ P, if (t,λ) ∈ δ (q,a,z), where a ∈ T ∪ {λ}.
Grammar G simulates the work of the PDAe in the following way: During the generating process the prefix of the generated word contains the the first part of the input word - which is already read by the pushdown automaton. It is followed by a nonterminal word A[q,z1,q1] A[q1,z2,q2]... A[qn-1,zn,qn], where z1z2... zn is the word contained by the stack, q is the current state and q1,q2,... qn can be any state. A[q,z,t] meaning that the automaton moves from state q to state t and removes the stack symbol z. The generated word keeps this structure during the generating process. When the automaton reaches the end of the input word and its stack is empty, then the word generated by the grammar contains the whole input word and does not contain any nonterminal symbols.
QED.
Lemma 4. For each context-free grammar G = (N, T, S, P) we can give a pushdown automaton PDAe = (Q, T, Z, q0, z0, δ) such that L(PDAe) = L(G).
Proof. The set of input letters of the PDAe and the set of terminal symbols of grammar G are the same. Let Q = {q0}, Z = N ∪ T, , and z0 = S. The production rules are very simple.
Let (q0,r) ∈ δ (q0,λ,A), if A → r ∈ P, and
let (q0,λ) ∈ δ (q0,a,a) for each a ∈ T.
During the computation of the PDAe, we use λ-steps to simulate the work of grammar G. The current word is always in the stack memory. We can remove the letters one by one, reading them from the input and clearing them at the same time from the top of the stack. The process is finished, when each letter is read and the stack is empty.
QED.
Theorem 23. A language is context-free, if and only if it is accepted by some pushdown automaton.
Proof. This theorem is a direct consequence of Lemma 3. and Lemma 4.
QED.
Finally, we have to note that for each context-free language we can give a pushdown automaton, which has only one state and accepts the context-free language by empty stack. This statement is a direct consequence of the proof of Lemma 4.
Definition 23. The pushdown automaton PDAd = (Q, T, Z, q0, z0, δ, F) is deterministic, if
δ(q,a,z) has at most one element for each triple q ∈ Q, a ∈ T ∪ {λ}, and z ∈ Z, and
if δ(q,λ,z), q ∈ Q, z ∈ Z has an element, then δ(q,a,z) = ∅ for each a ∈ T.
The language class accepted by deterministic pushdown automata with final states is a proper subset of the language class accepted by pushdown automata.
Definition 24. The class of languages accepted by deterministic pushdown automata is called the class of deterministic context-free languages.
In section 4.6.1. we have proven that the language class accepted by pushdown automata by final states and the language class accepted by pushdown automata by empty stack are the same. However, it is different for the deterministic case. The language class accepted by deterministic pushdown automata with empty stack is a proper subset of the language class accepted by deterministic pushdown automata with final states. Let us mark the deterministic pushdown automata accepting by empty stack with PDAde. We can summarize these properties in the following expression:
L (PDAde) ⊂ L (PDAd) ⊂ L (PDAe) = L (PDA).
In this subsection, we define a subclass of pushdown automata as it has already been mentioned in Subsection 3.2.
Definition 25. The one-turn pushdown automaton (OTPDA) is a pushdown automaton PDA = (Q, T, Z, q0, z0, δ, F) with the following property:
The set of states Q = Q1 ∪ Q2, where Q1 ∩ Q2 = ∅,
q0 ∈ Q1 is the initial state,
δ : Q × {T ∪ {λ}} × Z → 2Q×Z* is the transition function such that each of its transitions is
either of the form (q',z') ∈ δ (q,a,z) with q ∈ Q1, ,q' ∈ Q, a ∈ T ∪ {λ}, z ∈ Z, z' ∈ Z+,
or of the form (q',z') ∈ δ (q,a,z) for q, q' ∈ Q2, a ∈ T ∪ {λ}, z ∈ Z, z' ∈ Z ∪ {λ}.
According to the above definition, it is clear that in a run once the automaton reaches a state q' ∈ Q2, then it can never go back to a state in Q1: after the stack content has been decreasing in a step, it cannot increase again. This fact also appears in the name of these special automata: their runs have (at most) one turn point (measuring the stack content).
Example 51. Let PDA = ({q0,q1,qf}, {0,1,2 }, {y,z}, q0, z,δ, qf) be a one-turn pushdown automaton with
Q1 = {q0}, Q2 = {q1,qf},
and δ is given by the following transitions:
(q1,z) ∈ δ (q0,2,z), (q0,yz) ∈ δ (q0,0,z), (q0,yy) ∈ δ (q0,0,y), (q1,y) ∈ δ (q0,2,y), (q1, λ) ∈ δ (q1,1,y), (qf, λ ) ∈ δ(q1,2,z).
(For all other triplets of {q0,q1,qf} × {0,1,2} × {y,z} there is no transition available. Thus, if PDA reaches a configuration defining a triplet non-listed above, it causes the process to stop without accepting.)
The work of the automaton can be described as follows:
if the input is 22, then by reading the first 2, it changes its state to q1 (first transition) and then, it reaches qf by the last transition, and thus this input is accepted. (Observe that no other input starting with 2 can be accepted.)
if the input is of the form 0n21n2, then by the second transition PDA is starting to count and by the third transition it is continuing to count the number of 0's by pushing as many y's into the stack as the number of 0's already read. Then, by reading a 2 PDA is at its turning point (having n y in the stack), and it changes its state to q1. (Observe that there were no transitions defined for reading a 1 before this point.) Then, PDA is reading 1's and counting their number by decreasing the number of y's in the stack (popping them out one by one). Finally, if and only if the number of 0's are the same as the number of 1's, then PDA can accept the output by reading the last 2.
PDA is not accepting any other input.
Thus, this pushdown automaton accepts the language
L (PDA) = {0n21n2∣n ∈ ℕ}.
We are going to present the following theorem without a proof.
Theorem 24. The class of languages accepted by one-turn pushdown automata and the class of linear languages coincide.
If there is at most one possible transition in every possible configuration of a one-turn pushdown automaton, then it is a deterministic one-turn pushdown automaton. Observe that PDA is deterministic in Example 51. The deterministic variant of the one-turn pushdown automaton is weaker than the non-deterministic one, and thus the class of them accepts a proper subclass of linear languages, namely, the deterministic linear languages.
Example 52. The language
{anbn∣n ∈ ℕ} ∪ {anb3n∣n ∈ ℕ}
is a union of two languages that are deterministic linear, however, it is not deterministic linear itself.
This chapter is concluded by some exercises.
Exercise 67. Give a one-turn pushdown automaton that recognizes the language of palindromes (a palindrome is a word that is identical to its reverse). (Hint: this language cannot be accepted by deterministic OTPDA.)
Exercise 68. Give a deterministic one-turn pushdown automaton that recognizes the language
{anbmc2n+3∣ n, m ∈ ℕ}
over the alphabet {a,b,c}.
Exercise 69. Give a one-turn pushdown automaton that accepts the language
{uc*(c+d)ddv∣u, v ∈ {a,b}* such that the number of a's in u and v are the same}.
Table of Contents
Summary of the chapter: In this chapter, we deal with a family of languages generated by context-sensitive grammars of the Chomsky hierarchy, i.e., the context-sensitive languages. We are going to prove that monotone grammars generate the same language class. Normal forms of these grammars, such as Kuroda and Révész normal forms are provided. An example for a non-context-free, context-sensitive language is also given. The language class accepted by linear bounded automata coincides with the class of context-sensitive languages. This class is closed under the regular operations (union, concatenation, Kleene-star) and under the set theoretic operations complement and intersection. The word problem is solvable for these languages but no efficient algorithm is known for the general case.
For better understanding, we start this section by recalling the definition of context-sensitive grammars and languages.
Definition 26 (Context-sensitive grammars). A grammar G = (N, T, S, P) is context-sensitive if each of its productions has one of the following forms: pAq → puq, where A ∈ N, p, q ∈ (N ∪ T)*, u ∈ (N ∪ T)+; S → λ, and if S →λ ∈ P, then S does not occur in the right hand side of any rule in P. The languages that can be generated by context-sensitive grammars are the context-sensitive languages.
Example 53. Animation 9. shows an example for a context-sensitive grammar with a sample derivation.
We present yet another definition:
Definition 27. (Monotone grammars). A grammar G = (N, T, S, P) is monotone (or length-non-decreasing) if for each of its rules p → q (p ∈ (N ∪ T)* N (N∪T)*, q ∈ (N ∪ T)+)∣p∣ ≤ ∣q∣, but the possible rule S →λ. If S → λ is contained in P, then S does not occur in the right hand side of any rules of the grammar.
It is an interesting property of monotone grammars that the terminals can be rewritten: this definition is so general that it allows to this (if there is a nonterminal close to that terminal), for example, by rule aaaaB → cccCCcc (with a, c ∈ T; B, C ∈ N).
According to the definitions, it is obvious that every context-sensitive grammar is monotone. The opposite will also be proven in this section, but first we are going to investigate a few normal forms.
In this subsection, two normal forms are presented.
Definition 28. (Kuroda normal form). A monotone grammar G = (N, T, S, P) is in Kuroda normal form, if it is monotone, and each of its rules is in one of the following forms:
AB → CD, A → BC, A → B, A → a, S → λ
(A,B,C,D ∈ N, a ∈ T).
Since grammars in Kuroda normal form are monotone, in case S → λ is in the set of productions, the start symbol S cannot be in any right hand side of a rule. Kuroda normal form is a normal form, therefore we have the following theorem:
Theorem 25. There is an equivalent grammar in Kuroda normal form for every monotone grammar.
Proof. Let a monotone grammar G = (N, T, S, P) be given. The proof is constructive: we present an algorithmic way to obtain the grammar in Kuroda normal form that is equivalent to G. Since G is monotone, the generated language L(G) contains the empty word λ, if and only if there is a production S → λ in G. We need to deal only with the rules of the form p → q with ∣p∣ ≤ ∣q∣.
As a first step of our proof (algorithm), we obtain a grammar G'' that generates the same language as G, moreover, it has rules containing terminals only in rules of the form A → a. So for each terminal a let us introduce a new nonterminal Xa (Xa ∉ N), and replace each occurrence of all terminals in every rule by their new nonterminals (for example, a is replaced by Xa in every rule, both left and right hand side); and add the rules of the form Xa → a to the set of productions for each terminal:
N'' = N ∪{Xa∣a ∈ T},
G'' = (N'', T, S,
{p' → q'∣p → q ∈ P, and p' and q' are obtained from p and q, respectively, by replacing the occurrences of each terminal to the appropriate new nonterminal} ∪ {Xa → a∣a ∈ T}).
Observe that in G'' only nonterminals are rewritten. It can be seen that G' generates the same language as G, and the terminals can be derived only in the last steps of the derivations.
Now, if a rule of the monotone grammar G'' is not allowed to be in a grammar in Kuroda normal form, then this rule must have longer right hand side than it is allowed in Kuroda normal form (i.e., 2). Let us substitute each of these rules by a sequence of appropriate rules.
Let a rule A1... Am → B1... Bn in P. Based on the definition of monotone grammars it is clear that m ≤ n. Then
if n ≤ 2, then the rule is allowed in Kuroda normal form, and we leave it as is.
if m = 1 and n < 2, we can do the same replacement as we have done at the Chomsky normal form for context-free grammars (see the proof of Theorem 16.):
A1 → B1... Bn
is replaced by the set of rules
A1 → B1X1, X1 → B2X2, ... Xn-2 → Bn-1Bn,
where X1,...,Xn-2 are new nonterminals, were not in the grammar so far.
if m ≥ 2, n > 2, then
A1... Am → B1... Bn
is replaced by the set of rules
A1A2 → B1X1, X1A3 → B2X2, ... Xm-2Am → Bm-1Xm-1,
Xm-1 → BmXm, ... , Xn-2 → Bn-1Bn,
where X1,...,Xn-2 are new nonterminals, not used in the grammar before. See also Figure 5.1.
Figure 5.1. In derivations the rules with long right hand side are replaced by chains of shorter rules.
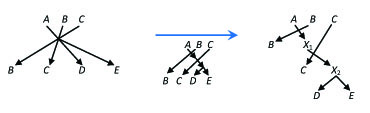
The resulting grammar generates the same language as G, and it is in Kuroda normal form.
QED.
Example 54. Let
G = ({S, A, B, C}, {0,1,2}, S,
{S → ABAB00,
ABA → A111A,
A111 → B221,
B → 2, B → CC,
BB → CBA,
C → S,
C → 021
}). Give a Kuroda normal form grammar that is equivalent to G.
Solution:
In the first step, by introducing the nonterminals D0, D1, D2 (using them instead of the terminals) we obtain G'' as follows:
G'' = ({S, A, B, C , D0, D1, D2}, {0,1,2}, S,
{S → ABABD0D0,
ABA → AD1D1D1A,
AD1D1D1 → BD2D2D1,
B → D2, B → CC,
BB → CBA,
C → S,
C → D0D2D1,
D0 → 0,
D1 → 1,
D2 → 2
}).Now, we need to replace the rules which have too many letters (having right hand side longer than 2):
| the original rule | replaced by the set of rules | |
| S → ABABD0D0: | S → AX1, X1 → BX2, X2 → AX3, X3 → BX4, X4 → D0D0, | |
| ABA → AD1D1D1A: | AB → AX5, X5A → D1X6, X6 → D1X7, X7 → D1A, | |
| AD1D1D1 → BD2D2D1: | AD1 → BX8, X8D1 → D2X9, X9D1 → D2D1, | |
| BB → CBA: | BB → CX10, X10 → BA, | |
| C → D0D2D1: | C → D0X11, X11 → D2D1. |
All the other rules are kept, thus we have the solution
G' = ({S, A, B, C, D0, D1, D2, X1, X2, X3, X4, X5, X6, X7, X8, X9, X10, X11}, {0,1,2}, S,
{S → AX1, X1 → BX2, X2 → AX3, X3 → BX4, X4 → D0D0,
AB → AX5, X5A → D1X6, X6 → D1X7, X7 → D1A, AD1 → BX8,
X8D1 → D2X9, X9D1 → D2D1, B → D2, B → CC, BB → CX10, X10 → BA,
C → S, C → D0X11, X11 → D2D1, D0 → 0, D1 → 1, D2 → 2}).
The next observation was proven by György Révész, so this normal form is caled Révész normal form. Every rule AB → CD of a Kuroda normal form grammar can be replaced by a chain of rules
AB → AX, AX → YX, YX → YD, YD → CD,
where X and Y are newly introduced nonterminals that are used only in these rules in the new grammar.
Definition 29. (Révész normal form). A grammar G = (N, T, S, P) is in Révész normal form, if each of its rules is in one of the following forms:
AB → AC, AB → CB, A → BC, A → B, A → a, S → λ
(A,B,C ∈ N, a ∈ T and S does not occur in the right hand side of any rule if S → λ ∈ P).
By using Révész's observation the following result is obtained:
Theorem 26. There is an equivalent grammar in Révész normal form for every monotone grammar.
Example 55. Let
G = ({S, A, B}, {a,b,c}, S,
{S → BaB,
BaB → BABa,
A → BbB,
A → c,
B → BABB,
B → AbbA,
B → aB,
B → c,
S → λ
}). Give a Révész normal form grammar that is equivalent to G.
Solution:
First, we obtain grammar G' that is in Kuroda normal form and generates the same language as G. Thus,
G'' = ({S, A, B, Ca, Cb, Cc}, {a,b,c}, S,
{S → BCaB,
BCaB → BABCa,
A → BCbB,
A → Cc,
B → BABB,
B → ACbCbA,
B → CaB,
B → Cc,
S → λ
}), and G' = ({S, A, B, Ca, Cb, Cc, X1, X2, X3, X4, X5, X6, X7, X8}, {a,b,c}, S,
{S → BX1, X1 → CaB,
BCa → BX2, X2B → AX3, X3 → BCa,
A → BX4, X4 → CbB,
A → Cc,
B → BX5, X5 → AX6, X6 → BB,
B → AX7, X7 → CbX8, X8 → CbA,
B → CaB,
B → Cc,
S → λ
}).Further, we need to replace the following rule by a chain of rules:
| the original rule | replaced by the set of rules | |
| X2B → AX3 | X2B → X2Y1, X2Y1 → Y2Y1, Y2Y1 → Y2X3, Y2X3 → AX3. |
Thus, the Révész normal form grammar that is equivalent to G is
G''' = ({S, A, B, Ca, Cb, Cc, X1, X2, X3, X4, X5, X6, X7, X8, Y1, X2}, {a,b,c}, S,
{S → BX1, X1 → CaB, BCa → BX2,
X2B → X2Y1, X2Y1 → Y2Y1, Y2Y1 → Y2X3, Y2X3 → AX3
X3 → BCa, A → BX4, X4 → CbB, A → Cc,
B → BX5, X5 → AX6, X6 → BB,
B → AX7, X7 → CbX8, X8 → CbA, B → CaB, B → Cc, S → λ}).
One may observe that grammars in Révész normal form satisfy the conditions of the definition of context-sensitive grammars, and thus one can construct an equivalent context-sensitive grammar for any monotone grammar, i.e., the following theorem is proven.
Theorem 27. The class of languages generated by monotone grammars coincides with the class of context-sensitive languages.
By the previous theorem, we may use any monotone grammar to generate a context-sensitive language.
As we have shown by the Empty-word lemma (Theorem 1.) every context-free language can be generated by context-sensitive grammars. Now, we are going to give an example that proves that the class of context-free languages is strictly included in the class of context-sensitive languages.
G = ({S, A, B, C}, {a,b,c}, S,
{S → λ,
S → abc,
S → aABC,
A → aABC,
A → aBC,
CB → BC,
aB → ab,
bB → bb,
bC → bc,
cC → cc
}). Then λ and abc can be derived directly from S. Then every other (finished) derivation in this grammar applies S → aABC, and then n times the rule A → aABC (n ∈ ℕ, n ≥ 0) and finally the rule A → aBC. In this way the sentential form starts with n + 2 a's and it contains n + 2 B's and C's. Then, every B must be positioned before the C's in a terminating derivation. Hence the generated language is {ajbjcj∣j ∈ ℕ}. See Animation 10. for a terminal derivation in this grammar.
Remember that in Example 41. we have shown that this language is not context-free, but as it can be seen from Example 56., it is context-sensitive.
We finish this section with some exercises.
Exercise 70. Give a monotone grammar that generates the language
{anbmcndm∣n, m ∈ ℕ}.
Exercise 71. Let
G = ({S, A, B}, {0,1}, S,
{S → SAS,
SA → B0B0S,
S → 1,
A → S0S,
B0B0 → 0S0S
}).Give a Kuroda normal form grammar that is equivalent to G.
Exercise 72. Let
G = ({S, A, B, C}, {d,e}, S,
{S → λ,
S → BeBe,
C → BeBe,
BeBe → dAdA,
eB → dede,
Bd → CAC,
A → ede,
B → dd
}). Give a Révész normal form grammar that generates the same language as G.
Exercise 73. Let
G = ({S, A, B, C, D}, {a,b,c}, S,
{S → λ,
S → AaBb,
Aa → ccBbBb,
Bb → CACA,
bB → DaDa,
DaD → CAC,
bBbBb → ABCaD,
A → a,
B → bb,
C → D,
C → ccc
}).Give a Révész normal form grammar that generates the same language as G.
Exercise 74. Let
G = ({S, A, B, C}, {a,b,c,d}, S,
{S → BBC,
S → SAB,
A → cdC,
cdA → CBbb,
Bb → aa,
bbA → dbd,
A → a,
A → d,
B → b,
C → SdS,
C → cd
}).Give a grammar in Révész normal form that generates the same language as G.
We mention here that a special class of Turing machines, the class of linear bounded automata recognizes exactly the class of context-sensitive languages. All the details will be shown in Subsection 6.4., when the concept of the Turing machines have already been introduced.
In this section, we prove that the class of context-sensitive languages is closed under union, concatenation and Kleene-star. It is also closed under the other set theoretical operations.
Theorem 28. The class of context-sensitive languages is closed under the regular operations.
Proof. The proof is constructive. Let L1 and L2 be two context-sensitive languages. Let the monotone grammars G1 = (N1, T, S1, P1) and G2 = (N2, T, S2, P2) be in Kuroda normal form and generate the languages L1 and L2, respectively, such that N1 ∩ N2 = ∅ (this can be done by renaming nonterminals of a grammar without affecting the generated language).
First, we show the closure under union.
If λ ∉ L1 ∪ L2, then let
G = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1, S → S2}),
where S ∉ N1 ∪ N2, a new symbol. It can be seen that G generates the language L1 ∪ L2.
If λ ∈ L1 ∪ L2 (i.e., S1 → λ ∈ P1 and/or S2 → λ ∈ P2), then let
G = (N1 ∪ N2 ∪ {S}, T, S,
P1 ∪ P2 ∪ {S → S1, S → S2, S → λ} \ {S1 → λ, S2 → λ}),
where S ∉ N1 ∪ N2. In this way, G generates the language L1 ∪ L2.
The closure under concatenation is proven for the following four cases:
If λ ∉ L1 and λ ∉ L2, then let
G = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1S2}),
where S ∉ N1 ∪ N2 a new symbol.
If λ ∈ L1 and λ ∉ L2, then let
G = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1S2, S → S2} \ {S1 → λ}),
where S is a new symbol.
If λ ∉ L1 and λ ∈ L2, then let
G = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1S2, S → S1} \ {S2 → λ}),
where S ∉ N1 ∪ N2 a new symbol.
If λ∈ L1 and λ ∈ L2, then let
G = (N1 ∪ N2 ∪ {S}, T, S,
P1 ∪ P2 ∪ {S → S1S2, S → S1, S → S2, S → λ} \ {S1 → λ, S2 → λ}),
where S ∉ N1 ∪ N2.
It can be easily seen that G generates the language L1L2.
Finally, let us consider the closure under Kleene-star. Let now G1 = (N1, T, S1, P1) and G2 = (N2, T, S2, P2) be in Kuroda normal form and generate the languages L (both G1 and G2) such that N1 ∩ N2 =∅.
Let
G = (N1 ∪ N2 ∪ {S, S'},
P1 ∪ P2 ∪ {S → λ, S → S1, S → S1S2, S → S1S2S', S' → S1, S' → S1S2, S' → S1S2S'} \ {S1 → λ, S2 → λ}),
where S, S' ∉ N1 ∪ N2, they are new symbols. Then G generates the language L*.
QED.
The closure of the class of context-sensitive languages under complementation was a famous problem and was open for more than 20 years. In the 1980's, Immerman, Szelepcsényi solved this problem independently. We present this result without proof.
Theorem 29. The class of context-sensitive languages is closed under complementation.
Theorem 30. The class of context-sensitive languages is closed under intersection.
Proof. The proof uses the fact that this class is closed both under union and complementation. Let us consider the context-sensitive languages L1 and L2. Then, the complement of each of them is context-sensitive according to the theorem of Immerman and Szelepcsényi. Their union is also context-sensitive, as we have proven constructively. The complement of this language is also context-sensitive. However, this language is the same as L1 ∩ L2 by the De Morgan law.
QED.
Exercise 75. Give a monotone grammar that generates the language of marked-copy:
{wcw∣w ∈ {a,b}*}
over the alphabet {a,b,c}. (Hint: use context-sensitive rules to allow some nonterminals to terminate, i.e., to change them to terminals only at the correct place.)
Exercise 76. Give context-sensitive grammars that generate the union and the concatenations of the languages generated by grammars G1 and G2, where
G1 = ({S1, A1, B1, C1}, {a,b,c}, S1,
{S1 → λ,
S1 → C1aA1,
S1 → B1,
aA1 → B1B1,
B1 → B1b,
B1bb → cba,
C1 → cA1
}) andG2 = ({S2, A2, B2, C2}, {a,b,c}, S2,
{S2 → cccS2aA2a,
S2 → bA2,
ccS2 → C2bA2,
bA2 → A2b,
A2 → cB2C2a,
A2 → aa,
cB2 → bB2,
bB2 → baccabB2,
C2 → C2c,
C2c → A2S2,
C2cc → cccc
}).Exercise 77. Let
G1 = ({S, A, B}, {0,1}, S,
{S → λ,
S → AB,
A → 0AB,
0A→ 1A,
AB → 11
}) andG2 = ({S, B, C, D}, {0,1}, S,
{S → λ,
S → BC,
S → D,
B → BC,
B → 1,
1C → 1D0,
D → DD,
D → 11,
1D → C0,
BDC → 00D11
}).Give context-sensitive grammars that generate
L(G1) ∪ L(G2),
L(G1) L(G2),
L(G2) L(G1),
(L(G1))* and
(L(G2))*.
The word problem of context-sensitive grammars can be solved. Since this language class is accepted by linear bounded automata, it can be solved in linear space in a nondeterministic manner. It is known that polynomial space is sufficient with a deterministic algorithm: the required space is c∣w∣2, where c is a constant and ∣w∣ is the length of the word. It is an open problem if linear space (i.e., c ∣w∣ with a constant c ) is sufficient or not. Regarding time complexity, there is no deterministic or nondeterministic algorithm is known that can solve the word problem in polynomial time (for arbitrary context-sensitive grammar/language).
Now, we are going to present a naive solution to the word problem (which is very inefficient), but at the same time it shows that the problem is solvable. So let G = (N, T, S, P) and w be given. If the input word is the empty word (w = λ), then it is in the language, if and only if S → λ ∈ P. If ∣w∣ > 0, then we may consider only the rules u → v of P with the property ∣u∣ ≤ ∣v∣. Then, let us use a bread-first search algorithm. Let the initial node of the graph be labeled by S. Consider the productions as possible operators on the sentential forms. Then, the search-graph can be obtained by applying every applicable rule for every node. This graph is usually infinite, but we need to obtain only a finite portion of it. (Every label must appear at most once in the graph.) Since each of the rules has the monotone property we may cut those branches of the search-space that contain a longer sentential form than w (the solution cannot be in the continuation of such a branch). When we have obtained all the portions of the search-graph representing sentential forms not longer than w, then we can check whether w is a node of the graph, or not. If so, then it can be derived, it is in the generated language, else it is not.
Exercise 78. Check whether the words abc and ccc are in the language generated by the grammar
G = ({S, A, B, C, D, E}, {a,b,c}, S,
{S → ab,
S → BS,
S → ABS,
A → a,
A → BCE,
AB → BA,
B → b,
BC → bc,
CE → abc,
D → b,
ED → aE,
E → DD,
bA → SS
}). Table of Contents
Summary of the chapter: In this chapter, we discuss the most universal language class, the class of recursively enumerable languages, and the most universal automaton, the Turing machine. In the first section, we investigate the recursive and the recursively enumerable languages, and their closure and other properties. The second and third section is dedicated to the Turing machine. We will show two different applications. First, we are going to use the Turing machine as a universal language acceptor, then we show how we can use it as a simple but universal computing device.
At the beginning of this chapter we introduce the recursive languages and the recursively enumerable languages. These two language classes are fundamental in computability theory. There are many equivalent definitions, however, we are going to use these two definitions now, and we are going to show how these definitions fit for the concept of the Turing machine later.
Definition 30. The language L ∈ V* is recursive, if there is an algorithm, which decides about any word p ∈ V*, whether or not p ∈ L.
We can say a language L is recursive, if the word problem can be solved in L. In Chapter 1. we define the class of the recursively enumerable languages as languages which can be generated by unrestricted generative grammars. Now, we give another definition.
Definition 31. The language L ∈ V* is recursively enumerable, if there is a procedure, which specifies all the elements of L.
The two definitions of the recursively enumerable languages are equivalent. If there is a procedure, which specifies all elements of the language L, then there is a generative grammar which generates the language L, and if there is a generative grammar generating the language L, then this grammar itself is a procedure, which can be used to specify all elements of the language L.
It is obvious that each recursive language is a recursively enumerable, because we can list the words over an alphabet V, and select those words which are contained by the language L.
Theorem 31. The language L is recursive, if and only if both L and 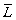 are recursively enumerable.
are recursively enumerable.
Proof. First, we show that, if L ∈ V*
and 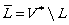 are recursively enumerables, then L - and also
are recursively enumerables, then L - and also 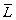 - is recursive. The language L is recursively enumerable,
so there is a procedure which lists the elements of L. Let us denote these words p1,
p2,....
However,
- is recursive. The language L is recursively enumerable,
so there is a procedure which lists the elements of L. Let us denote these words p1,
p2,....
However, 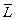 is recursively enumerable as well, so we have another procedure which lists
the elements of
is recursively enumerable as well, so we have another procedure which lists
the elements of 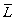 . Let us denote these words r1,r2,....
Now we can combine these two
procedures, to use the first one, and then the second one, alternately. What we receive is the list of all words over the
alphabet V: p1, r1, p2,
r2,... and we know about each one if it belongs to the language L or not.
. Let us denote these words r1,r2,....
Now we can combine these two
procedures, to use the first one, and then the second one, alternately. What we receive is the list of all words over the
alphabet V: p1, r1, p2,
r2,... and we know about each one if it belongs to the language L or not.
Now, we show that if L is recursive, then L and 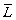 is recursively enumerable.
We already mentioned that recursive languages are recursively enumerable, because we can
list all the words over an alphabet V, and add the current word to the language if it is in L. The same
algorithm can be used for the language
is recursively enumerable.
We already mentioned that recursive languages are recursively enumerable, because we can
list all the words over an alphabet V, and add the current word to the language if it is in L. The same
algorithm can be used for the language 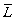 , we can list the words again, and we add
them to the language if they are not in the language L.
, we can list the words again, and we add
them to the language if they are not in the language L.
QED.
The following theorem shows the connection between the context-sensitive and recursive languages.
Theorem 32. Each context-sensitive language is recursive, but there are recursive languages which are not context-sensitive.
Proof. The first part of the theorem states that the word problem can be solved for each context-sensitive language. This was shown already in Section 5.3.2.
For the second part, let us create the list of each possible context-sensitive generative grammar Gi = (Ni, Ti, Si, Pi), which generates numbers. (The set of the terminal letters of each grammar Gi are digits, so Ti = {0,1,2,3,4,5,6,7,8,9} for each Gi.) Now, we define language L, which contains the sequential numbers of grammars whose generated language does not contain its own sequential number (position in the list): L = {i∣i ∉ L(Gi)}.
We can create a list of all context-sensitive generative grammars which generates numbers, and we can decide whether or not a context-sensitive grammar generates its position in the list, so language L is recursive.
Now, suppose to the contrary that language L is context-sensitive. In this case, there is a context-sensitive grammar Gk, such that L(Gk) = L. Then, by the definition of L, if k ∈ L(Gk), then k ∉ L is a contradiction, and if k ∉ L(Gk), then k ∈ L is also a contradiction. The only possible solution is that language L is not context-sensitive.
QED.
The next theorem shows that there are languages which are not in the class of recursively enumerable languages, so the recursively enumerable language class does not contain all possible languages. The concept of the proof is similar to the previous proof.
Theorem 33. There exists a language L, which is not recursively enumerable.
Proof. Let us create the list of each generative grammar Gi = (Ni, Ti, Si, Pi) which generates numbers. (The set of the terminals of each grammar Gi are numbers: Ti = {0,1,2,3,4,5,6,7,8,9} for each grammar Gi). We have to note that it is easy to create an ordered list of all possible generative grammars which generates numbers. Now, we define language L, which contains the numbers of the grammars which does not generate the number of its position in the list: L = {i∣i ∉ L(Gi)}.
Now, suppose to the contrary that the language L is recursively enumerable. In this case, there is a generative grammar Gk, such that L(Gk) = L. Then, by the definition of L, if k ∈ L(Gk), then k ∉ L is a contradiction, and if k ∉ L(Gk), then k ∈ L is also a contradiction. The only possible solution is that language L is not recursively enumerable.
QED.
We have already shown that the class of context-sensitive languages is a proper subset of the class of recursive languages. It has also been proven that the class of all languages is a proper superset of the class of recursively enumerable languages. Finally, we note that the complementer language of language L defined in the proof of Theorem 33. is recursively enumerable, but not recursive. We can summarize our results in the following formula:
CS ⊊ R ⊊ RE ⊊ AL
where CS stands for context-sensitive languages, R stands for recursive languages, RE stands for recursively enumerable languages, and AL stands for all languages.
Theorem 34. The class of recursive languages is closed under complement operation.
Proof. Theorem 31. states that language L is recursive,
if and only if L and 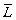 are both recursively enumerable. However, we can apply the same theorem for the language
are both recursively enumerable. However, we can apply the same theorem for the language 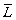 ,
and what we receive as a result is that
,
and what we receive as a result is that 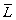 is recursive, if
is recursive, if 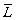 and L are both recursively
enumerable, which is the same condition, so if L is recursive, then
and L are both recursively
enumerable, which is the same condition, so if L is recursive, then 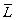 is recursive, as well.
is recursive, as well.
QED.
Theorem 35. The class of recursively enumerable languages is not closed under complement operation.
Proof. The proof of this theorem is easy, we need only one example, where the language itself is recursively
enumerable, and the complement language is not recursively enumerable. In the proof of the Theorem 33.
we have defined a language L which is not recursively
enumerable. The complement language 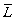 is recursively enumerable. Here we have a recursively
enumerable language
is recursively enumerable. Here we have a recursively
enumerable language 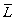 , whose complement is not recursively enumerable.
, whose complement is not recursively enumerable.
QED.
Theorem 36. The class of recursively enumerable languages is closed under regular operations.
Proof. We give a constructive proof here. Let the languages L1 and L2 be recursively enumerable. Let the grammar G1 = (N1, T, S1, P1) such that L(G1) = L1, and let the grammar G2 = (N2, T, S2, P2) such that L(G2) = L2. Without loss of generality we can suppose that N1 ∩ N2 =∅, and the terminal symbols appear only in rules having the form A → a, where A ∈ N, a ∈ T. We define generative grammars GUn, and GCo, such that L(GUn) = L1 ∪ L2, and L(GCo) = L1 · L2.
Union
Let S be a new start symbol, such that S ∩ N1 = S ∩ N2 = S ∩ T = ∅, and let
GUn = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1, S → S2}).
Concatenation
Let S be a new start symbol, such that S ∩ N1 = S ∩ N2 = S ∩ T = ∅, and let
GCo = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → S1S2}).
Kleene star
In order to create a grammar generating the language L(GKl) = L1* we use two grammars. Let the grammar G1 = (N1, T, S1, P1), and let the grammar G2 = (N2, T, S2, P2) such that L(G1) = L(G2) = L1 \ {λ}, and N1 ∩ N2 = ∅. Without loss of generality we can suppose that the terminal symbols appear only in rules having the form A → a, where A ∈ N, a ∈ T. For the grammar GKl we again use a new start symbol S, where S ∩ N1 = S ∩ N2 = S ∩ T = ∅. Then, let
GKl = (N1 ∪ N2 ∪ {S}, T, S, P1 ∪ P2 ∪ {S → λ, S → S1, S → S1S2S}).
QED.
Theorem 37. The class of recursively enumerable languages is closed under intersection.
Proof. By applying the definition of the recursively enumerable language, we can create a list of the elements of the recursively enumerable language L1 without repetitions, and yet another list, which contains the elements from the recursively enumerable language L2 without repetitions. Then, we can create a list, which contains one element from the list of the language L1, and then one element of the list of the language L2 alternately. We move an element from this combined list into the list of the L1 ∩ L2, if the element appears twice.
QED.
Finally, we have to note that recursive languages are also closed under regular operations and intersection.
Definition The grammar G = (N, T, S, P) is in Révész normal form, if all of its production rules has the following forms:
S → λ,
A → a,
A → B,
A → BC,
AB → AC,
AB → CB, or
AB → B,
where A, B, C ∈ N and a ∈ T.
This normal form for unrestricted grammars was introduced by György Révész. Compared to the Kuroda normal form, the differences are the following:
It allows the rule S → λ for grammars generating the empty word,
instead of the rule AB → CD it allows two rules, namely AB → AC and AB → CB,
the only ,,really plus'' rule, which makes the difference between the monotone and unrestricted grammars is the last production rule: AB → B.
As you can see, there is not a huge difference between the unrestricted grammars and the context-sensitive grammars. For generative grammars generating context-sensitive languages, only one production rule form is enough to be able to generate any recursively enumerable language.
Even more surprising results were proven by Viliam Geffert. His results put limitations not just to the form of the production rules, but also to the number of the nonterminal symbols. We introduce his results as theorems, without proofs.
Theorem 38. For each recursively enumerable language L we can give an unrestricted generative grammar G = (N, T, S, H) such that
grammar G generates the language L, (L(G) = L),
G has exactly 5 nonterminal symbols, (N = {S, A, B, C, D}), and
each rule has a form:
S → p where S is the start symbol, and p is a nonempty word, (p ∈ (N ∪ T)+),
AB → λ, or
CD → λ.
Theorem 39. For each recursively enumerable language L we can give an unrestricted generative grammar G = (N, T, S, H) such that
grammar G generates the language L, (L(G) = L),
G has exactly 4 nonterminal symbols, (N = {S, A, B, C}), and
each rule has a form:
S → p where S is the start symbol, and p is a nonempty word, (p ∈ (N ∪ T)+),
AB → λ, or
CC → λ.
Theorem 40. For each recursively enumerable language L we can give an unrestricted generative grammar G = (N, T, S, H) such that
grammar G generates the language L, (L(G) = L),
G has exactly 3 nonterminal symbols, (N = {S,A,B}), and
each rule has a form:
S → p where S is the start symbol, and p is a nonempty word, (p ∈ (N ∪ T)+),
AA → λ, or
BBB → λ.
Theorem 41. For each recursively enumerable language L we can give an unrestricted generative grammar G = (N, T, S, H) such that
grammar G generates the language L, (L(G) = L),
G has exactly 3 nonterminal symbols, (N = {S, A, B}), and
each rule has a form:
S → p where S is the start symbol, and p is a nonempty word, (p ∈ (N ∪ T)+), or
ABBBA → λ.
Theorem 42. For each recursively enumerable language L we can give an unrestricted generative grammar G = (N, T, S, H) such that
grammar G generates the language L, (L(G) = L),
G has exactly 4 nonterminal symbols, (N = {S, A, B, C}), and
each rule has a form:
S → p where S is the start symbol, and p is a nonempty word, (p ∈ (N ∪ T)+), or
ABC → λ.
Turing machines play a fundamental role in the algorithms and computational theory. The concept of Turing machine was invented by Alan Turing in 1937. This simple hypothetical device is able to compute all the functions which are algorithmically computable. Before we deal with the Turing machine as a universal tool for describing algorithms, we introduce the Turing machine as a universal language definition device.
The basic concept is that the Turing machine manipulates a string on a two-way infinite tape according to transition rules, and decides whether or not the input string belongs to a language accepted by the Turing machine. The tape contains an infinite number of cells, and each cell contains one letter. At the beginning, the tape contains the input string, and the rest of the cells contain a special tape symbol called a blank symbol. There is a head, which can read and write the content of the current cell of the tape, and can move both to the left and to the right. At the beginning, the head is over the first letter of the input string. The Turing machine also has its own inner state, which can be changed in each step. At the beginning, the inner state of the Turing machine is the initial state. The transition rules are the "program" of the Turing machine.
In each step the machine reads the letter contained by the current cell of the tape, and also reads its own inner state, then writes a letter into the current cell, changes its inner state and moves the head to the left or to the right, or stays in the same position. Sometimes, it does not change its inner state, and sometimes it does not change the content of the current cell. The operations of the Turing machine are based on the transition rules.
Let us see the formal definition and the detailed description.
Definition 33. The (nondeterministic) Turing machine (TM) is the following 7-tuple:
TM = (Q, T, V, q0, #, δ, F)
where
Q is the finite nonempty set of the states,
T is the set of the input letters, (finite nonempty alphabet), T ⊆ V,
V is the set of the tape symbols, (finite nonempty alphabet),
q0 is the initial state, q0 ∈ Q,
# is the blank symbol, # ∈ V,
δ is the transition function having a form Q × V → 2Q×V×{Left, Right, Stay}, and
F is the set of the final states, F ⊆ Q.
We have a description of the parts of our device, and now we have to describe its operation. In each step, the Turing machine has its configuration (u,q,av), where q ∈ Q is the current state, a ∈ V is the letter contained by the current cell, and u, v ∈ V* are the words before and after the current letter, respectively. The first letter of the word u and the last letter of the word v cannot be the blank symbol, and the word uav is the "important" part of the tape, the rest of the tape contains only blank symbols. At the beginning, the Turing machine has its initial configuration: (λ, q0, av), where av is the whole input word. In each step, the Turing machine changes its configuration according to the transition function. There are three possibilities, depending on the movement part of the applied rule.
The simplest case is when the applied transition rule has a form (q2, a2, Stay) ∈ δ (q1, a1). In this case, we just change the state and the symbol contained by the current cell of the tape according to the current rule. Formally, we say the TM can change its configuration from (u, q1, a1v) to (u, q2, a2v) in one step, if it has a transition rule (q2, a2, Stay) ∈ δ (q1, a1), where q1, q2 ∈ Q, a1, a2 ∈ V, and u, v ∈ V*.
Mark: (u, q1, a1v) ⊦TM (u, q2, a2v).
The next possibility is when the applied transition rule has a form (q2, a2, Right) ∈ δ (q1, a1). In this case, we change the state and the symbol contained by the current cell of the tape according to the current rule, and move the head to the right. Formally, we say the TM can change its configuration from (u, q1, a1v) to (ua2, q2, v) in one step, if it has a transition rule (q2, a2, Right) ∈ δ (q1, a1), where q1, q2 ∈ Q, a1, a2 ∈ V, and u, v ∈ V*.
It is denoted by (u, q1, a1v) ⊦TM (ua2, q2, v).
Here, we have a special case, namely, if a2 = # and u = λ, then (u, q1, a1v) ⊦TM (λ, q2, v).
The last possibility is when the applied transition rule has a form (q2, a2, Left) ∈ δ(q1, a1). In this case, we change the state and the symbol contained by the current cell of the tape according to the current rule, and move the head to the left. To formalize this case, we have to write the word u in a form u = wb, where b is the last letter of the word u. We say that the TM can change its configuration from (wb, q1, a1v) to (w, q2, ba2v) in one step, if it has a transition rule (q2, a2, Left) ∈ δ (q1, a1), where q1, q2 ∈ Q, a1, a2, b ∈ V, and w, v ∈ V*.
It is denoted by (wb, q1, a1v) ⊦TM (w, q2, ba2v).
Here, we also have a special case, namely, if a2 = # and v = λ, then (wb, q1, a1v) ⊦TM (w, q2, b).
Now, let X and Y be configurations of the same Turing machine. Then, we say that the Turing machine can change its configuration from X to Y in finite number of steps, if X = Y, or there are configurations C0, C1, ..., Cn such that C0 = X, Cn = Y, and Ci ⊦TM Ci+1 holds for each integer 0 ≤ i < n.
It is denoted by X ⊦*TM Y.
A configuration is called a final configuration, if the Turing machine is in a final state. Now, we can define the language accepted by the Turing machine. The input word is accepted, if the Turing machine can change its configuration from the initial configuration to a final configuration in finite number of steps.
L(TM) = {p∣p ∈ T*, (λ, q0, p) ⊦*TM (u, qf, av), qf ∈ F, a ∈ V, u, v ∈ V*}.
Example 57. Let the language L be the language of the palindromes over the alphabet {a, b}. (Palindromes are words that reads the same backward or forward.) This example shows the description of a Turing machine TM, which accepts the language L.
TM = ({q0,q1,q2,q3,q4,q5,qf}, {a,b}, {a,b,#}, q0,#,δ, {qf}) δ(q0,#) = {(qf,#,Stay)}, δ(q0,a) = {(q1,#,Right)}, δ(q0,b) = {(q2,#,Right}, δ(q1,a) = {(q1,a,Right)}, δ(q1,b) = {(q1,b,Right)}, δ(q1,#) = {(q3,#,Left)}, δ(q3,a) = {(q5,#,Left)}, δ(q3,#) = {(qf,#,Stay)}, δ(q2,a) = {(q2,a,Right)}, δ(q2,b) = {(q2,b,Right)}, δ(q2,#) = {(q4,#,Left)}, δ(q4,#) = {(qf,#,Stay)}, δ(q4,b) = {(q5,#,Left)}, δ(q5,a) = {(q5,a,Left)}, δ(q5,b) = {(q5,b,Left)}, δ(q5,#) = {(q0,#,Right)}.
Exercise 79. Create a Turing machine, which accepts words over the alphabet {a,b} containing the same number of a's and b's.
Exercise 80. Create a Turing machine, which accepts words over the alphabet {a,b} if they are a repetition of another word.
Exercise 81. Create a Turing machine, which accepts binary numbers greater than 20.
Our final note is that, although it is a simple construction, Turing machines can accept any language from the recursively enumerable language class. This statement is formulated in the following theorem.
Theorem 43. A language L is recursively enumerable, if and only if there exists a Turing machine TM such that L = L(TM).
There are several equivalent definitions for the Turing machine. In this subsection we are going to introduce some of them. Our first definition is the deterministic Turing machine, which has the same language definition power as the nondeterministic Turing machine. A Turing machine is called deterministic, if from each configuration it can reach at most one other configuration in one step. The formal definition is the following:
Definition 34 The Turing machine TMd = (Q, T, V, q0, #, δ, F) is deterministic, if the transition function δ(q,a) has at most one element for each pair (q,a), where q ∈ Q and a ∈ V.
In other words, the Turing machine TMd = (Q, T, V, q0, #, δ, F) is deterministic, if the form of the transition function δ is Q × V → Q × V × {Left, Right, Stay}.
Theorem 44. For each Turing machine TM there exists a deterministic Turing machine TMd such that L(TM) = L(TMd).
Now, we are going to introduce the multitape Turing machine, which looks like a more powerful tool compared to the original Turing machine, but in reality it has the same language definition power. In this case, we have more than one tape, and we work on each tape in each step. At the beginning, the input word is written on the first tape, and the other tapes are empty. (Contains blank symbols in each position.) The multitape Turing machine is in initial state, and the head is over the first letter of the first tape. In each step the multitape Turing machine reads its own state and the symbols from the cells of each tape, then changes its state; it writes symbols into the current cell of each tape and moves the head to the left or to the right, or stays in a same position over each tape separately. Observing the formal definition, its only difference compared to the deterministic Turing machine is that it has more tapes, and as a result, it has a different transition function.
Definition 35. The multitape Turing machine is the following octuple TMm = (k, Q, T, V, q0, #, δ, F), where Q, T, V, q0, # and F are the same as before, the integer k ≥ 0 is the number of the tapes, and the form of the transition function δ is Q × Vk → Q × (V × {Left, Right, Stay})k.
As we have noted before, multitape Turing machines accept recursively enumerable languages as well.
Theorem 45. For each multitape Turing machine TMm there exists (a one-tape) Turing machine TM such that L(TM) = L(TMm).
The reason for using the multitape Turing machine or the deterministic Turing machine instead of the original Turing machine is very simple. Sometimes it is more comfortable to use these alternative Turing machines for calculating or proving theorems.
For the same purpose, sometimes we use a Turing machine which has one tape, and this tape is infinite in one direction, and the other direction is "blocked". This version has a special tape symbol in the first cell, and when the Turing machine reads this symbol, the head moves to the right and does not change this special symbol. There is yet another possibility, when the Turing machine must not stay in the same position, in each step the head must move to the right or to the left. Sometimes we use only one final state, and sometimes we use a rejecting state as well, but all of these versions are equivalent to each other. Each of the Turing machine described above accepts recursively enumerable languages, and each recursively enumerable language can be accepted by each type of the above mention Turing machines.
We have discussed earlier that the Turing machine is not just a language definition tool. The original reason for introducing the Turing machine was to simulate mathematical algorithms which can calculate complicated functions. Later, it has been recognized that all algorithmically computable functions can be calculated by the Turing machine, as well. The statement which claims that a function is algorithmically computable if and only if it can be computed by the Turing machine is called Church's thesis. Church's thesis is not a theorem, it cannot be proven, because "algorithmically computable" is not a well defined expression in the thesis. In spite of the fact that Church's thesis is not a proven theorem, the thesis is accepted among scientists. The most important consequence of the thesis is that even the latest, and the strongest computer with a highly improved computer program can only compute the same things as a very simple Turing machine. Therefore we can use the Turing machine to show if something can be computed or not; and this is why the Turing machine plays a fundamental role in the algorithms and computational theory. Although this book focuses on formal languages, we cannot conclude this topic without illustrating the basics of the application of the Turing machine as a computing device.
When we use the Turing machine to compute/calculate a function, we use it the same way as before. At the beginning, the input word is on the tape, and when the Turing machine reaches a final configuration (u,qf,av), the result of the computation/calculation is the word uav, which is the significant part of the tape. In the Example 58. we show a Turing machine, which computes the two's complement of the input binary number.
Example 58. TM = ({q0, q1, qf}, {0,1}, {0,1,#}, q0, #, δ, {qf})
δ(q0,1) = {(q0,0,Right)}, δ(q0,0) = {(q0,1,Right)}, δ(q0,#) = {(q1,#,Left}, δ(q1,1) = {(q1,0,Left)}, δ(q1,0) = {(qf,1,Stay)}.
The Figure 6.1. shows the graphical notation of this Turing machine.
Exercise 82. Create a Turing machine, which changes the first five 0 to 1 in an input binary number.
Exercise 83. Create a Turing machine, which adds five to the input binary number.
Exercise 84. Create a Turing machine, which changes the order of two input binary numbers, separated by space.
Each equivalent definition of the Turing machine which was given at the end of the previous section can work here, so we can use the deterministic Turing machine, the multitape Turing machine, and the single tape Turing machine, which is infinite only in one direction, or we can extend the Turing machine with rejecting states, our choice will not influence the calculating power.
As we have already demonstrated, there are languages which are not recursively enumerable. This means that these languages cannot be generated by a generative grammar, and cannot be accepted by Turing machines. Also, there are functions, which cannot be computed by Turing machines. There is a well known example: the halting problem. There is a computer program given with an input, decide whether the program stops running after a while, or goes into an infinite loop. The same problem with Turing machine appears to be the following: given a description of a Turing machine and the input word, decide whether the Turing machine stops running or keeps on running forever. Let us denote the description of a Turing machine with dTM and the input word with w. The problem is to create a Turing machine which decides about each input word dTM#w whether or not the Turing machine TM goes into an infinite loop with the input word w. It has been shown that this problem cannot be decided by a Turing machine, so there is no universal algorithm to decide if a given computer program goes into an infinite loop or not. The equivalent problem is to create a Turing machine which accepts an input word dTM#w, if the Turing machine TM stops with the input word w. As one can see, computing/calculating a function or accepting a language is not so distant from each other. We also have to point out that the halting problem cannot be solved, because we suppose that the Turing machine has an infinite tape. The problem can be solved in a computer with a finite memory, however, the algorithm is not efficient in practice. We have already shown that there are functions which cannot be algorithmically computed, consequently there are problems which cannot be solved. However, there are many problems, which can be solved, and we would like to know the complexity of the algorithms computing the solutions. For this reason, scientists have introduced the time complexity of the algorithms. The time complexity of an algorithm is not a constant number. For a longer input the Turing machine needs longer time to compute, so the time complexity of an algorithm is a function for each algorithm, and the parameter of the function is the length of the input word w. This length is commonly denoted by n, so n = ∣w∣, and the time complexity of the Turing machine TM is denoted by T(n). We can investigate the space complexity of an algorithm as well. Let us denote by S(n) the function which shows how many cells we use on the tape of the Turing machine TM for an input word of length n. Of course, the time complexity and the space complexity are not independent from each other. If the time is limited, we have a limitation on the number of steps, so we can go to a limited distance from the initial position on the tape, which means that the space is also limited. The most important time complexity classes are the followings:
constant time, when the calculating time is fixed, does not depend on the length of the input, denoted by O(1),
logarithmic time, when the calculating time is not more than a logarithmic function of the length of the input word, denoted by O(log n),
linear time, when the calculating time is not more than a linear function of the length of the input word, denoted by O(n),
polynomial time, when the calculating time is not more than a polynomial function of the length of the input word, denoted by O(nk),
exponential time, when the calculating time is not more than an exponential function of the length of the input word, denoted by O(2nk).
Evidently, we can have the same complexity classes for the space used by a Turing machine, and most of our computer programs are deterministic, so these complexity classes can be similarly defined for deterministic Turing machines, as well. We know that the nondeterministic and the deterministic Turing machines have the same computational power, but we do not know if the problems which can be solved with nondeterministic Turing machines in polynomial time, and the problems which can be solved with deterministic Turing machines in polynomial time are the same or not. This is a major problem in algorithm theory, and it is called P = NP? problem.
Our last section is about the linear bounded automaton, which is a Turing machine with linear space complexity, and has a special role in the study of context-sensitive languages.
In this section, we present a special, bounded version of the Turing machines, by which the class of context-sensitive languages can be characterized - as we already mentioned in Subsection. This version of the Turing machine can work only on the part of the tape where the input is/was. These automata are called linear bounded automata (LBA).
Definition 36. Let LBA = (Q, T, V, q0, ♯, δ, F) be a Turing machine, where
δ : Q × (V \ {♯}) → 2Q×V×{Left, Right, Stay}
and
δ : Q × {♯} → 2Q×{♯}×{Left, Right, Stay}.
Then LBA is a (nondeterministic) linear bounded automaton.
One can observe that ♯ signs cannot be rewritten to any other symbol, therefore, the automaton can store some results of its subcomputations only in the space provided by the input, i.e., in fact, the length of the input can be used during the computation, only.
Example 59. Give an LBA that accepts the language {aibici∣i ∈ ℕ}.
Solution:
Idea:
The automaton rewrites the first a to A, and changes its state, looks for the first b.
The automaton rewrites the first b to B, and changes its state, looks for the first c.
The automaton rewrites the first c to C, and changes its state, looks (backward) for the first a.
The capital letters A,B,C are read without changing them.
The above movements are repeated.
If finally only capital letters remain between the border ♯ signs, then the automaton accepts (the input).
Formally, let
LBA = ({q0, q1, q2, q3, q4, qf}, {a,b,c}, {a,b,c,A,B,C,♯}, q0, ♯, δ, {qf})
be a deterministic LBA, where δ consists of the next transitions:
δ (q0, ♯) = (qf, ♯, Right) – the empty word is accepted by LBA.
δ (q0, a) = (q1, A, Right) – the first (leftmost) a is rewritten to A and LBA changes its state.
δ (q0, B) = (q0, B, Left) – the capital letters B and C are skipped in state q0,
δ (q0, C) = (q0, C, Left) – by moving the head to the left.
δ (q1, a) = (q1, a, Right) – letter a is skipped in state q1 to the right.
δ (q1, B) = (q1, B, Right) – capital B is also skipped.
δ (q1, b) = (q2, B, Right) – the leftmost b is rewritten by B and the state becomes q2.
δ (q2, b) = (q2, b, Right) – letter b is skipped in state q2 to the right.
δ (q2, C) = (q2, C, Right) – capital C is also skipped in this state.
δ (q2, c) = (q3, C, Left) – the leftmost c is rewritten by C and LBA changes its state to q3.
δ (q3, a) = (q3, a, Left) – letters a,b are skipped in state q3
δ (q3, b) = (q3, b, Left) – by moving the head of the automaton to the left.
δ (q3, C) = (q3, C, Left) – capital letters C,B are skipped in state q3
δ (q3, B) = (q3, B, Left) – by moving the head of the automaton to the left.
δ (q0, A) = (q3, A, Right) – the head is positioned after the last A and the state is changed to q0.
δ (q4, B) = (q3, B, Right) – if there is a B after the last A the state is changed to q4.
δ (q4, B) = (q4, B, Right) – in state q4 capital letters B and C are skipped
δ (q4, C) = (q4, C, Right) – by moving the head to the right.
δ (qf, ♯) = (q4, ♯, Left) – if in q4 there were only capital letters on the tape, LBA accepts.
The work of the automaton can be described as follows: it is clear by transition 1, that λ is accepted.
Otherwise the head reads the first letter of the input: if the input starts with an a, then it is replaced by A and q1 is the new state. If the first letter of the input is not a, then LBA gets stuck, i.e., it is halting without acceptance, since there are no defined transitions in this state for the other input letters.
In state q1 LBA looks for the first b by moving to the right (skipping every a and B, if any; and halting without acceptance by finding other letters before the first b). When a b is found it is rewritten to a B and the automaton changes its state to q2.
In q2 the first c is searched, the head can move through on b's and C's (but not on other letters) to the right. When it finds a c it rewrites by a C and changes the state to q3 and starts to move back to the left.
In q3 the head can go through on letters a,B,b,C to the left and when finds an A it steps to the right and the state becomes q0. In q0 if there is an a under the head, then it is rewritten by an A and the whole loop starts again.
If in q0 a letter B is found (that could happen when every a is rewritten by an A already), LBA changes its state to q4. In this state by stepping to the right LBA checks if every b and c is already rewritten and if so, i.e., their number is the same as the number of a's and their order was correct (the input is in the language a*b*c*), then LBA reaches the marker ♯ sign after the input and accepts.
When at any stage some other letter is being read than it is expected (by the previous description), then LBA halts without accepting the input.
Thus, the accepted language is exactly {aibici∣i∈ ℕ}.
To establish a connection between the classes of context-sensitive languages and linear bounded automata we present the following theorem.
Theorem 46. The class of languages accepted by linear bounded automata and the class of context-sensitive languages coincide.
Proof. We do not give a formal proof here, instead we present the idea of a proof. A context-sensitive language can be defined by a monotone grammar. In a monotone grammar (apart from the derivation of the empty word, if it is in the language), the length of the sentential form cannot be decreased by any step of the derivation. Consequently, starting from the derived word, and applying the rules in a way which is an inverse, the length is monotonously decreasing till we obtain the start symbol. In this way every context-sensitive language can be accepted by an LBA.
The other way around, the work of an LBA can be described by a grammar, working in inverse way of the generation (starting from a word the start symbol is the target). These grammars are similar to the previously used monotone grammars, and thus, if an LBA is accepting a language L, then L is context-sensitive.
QED.
Actually, there are other models of LBA, in which the workspace (the maximal tape-length during the computation) is limited by c1 · ∣w∣ + c0, where w is the input and c0, c1 ∈ ℝ constants. The accepting power of these models are the same as of those that have been presented.
However, the deterministic model is more interesting, since it is related to a long-standing and still open question.
It is known that every context-sensitive language can be accepted by deterministic Turing machines, using at most c2· ∣w∣2 + c1 · ∣w∣ + c0 space during the computations, where c2, c1, c0 are constants. However, it is neither proven nor disproved that deterministic linear bounded automata (using c1 · ∣w∣ + c2 space) can recognize every context-sensitive language. This is still a famous open problem.
Exercise 85. Give a linear bounded automaton that accepts the language
{aibjaibj∣i, j ∈ ℕ}.
Exercise 86. Give a linear bounded automaton that accepts the language
{a2i∣i ∈ ℕ},
i.e., the language of powers of two in unary coding.
Exercise 87. Give a linear bounded automaton that accepts the set of primitive words over the alphabet {a,b}. (A word w is primitive if it is not of the form un for any word u≠ w.)
For further reading the following books in related topics are recommended:
Bel-Enguix, Gemma, Jiménez-López, Maria Dolores and Martín-Víde, Carlos (eds.): Recent Developments in Formal Languages and Applications, Springer, Berlin, 2008.
Ésik, Zoltán, Martín-Vide, Carlos and Mitrana, Victor (eds.): Recent Advances in Formal Languages and Applications, Springer 2006.
Harrison, Michael A.: Introduction to Formal Language Theory, Addison-Wesley, 1978.
Herendi, Tamás and Nagy, Benedek: Parallel Approach of Algorithms, Typotex, Budapest, 2014.
Hopcroft, John E. and Ullmann, Jeffrey D.: Introduction to Automata Theory, Languages, and Computation. Addison-Wesley, Reading, Massachusetts, Menlo Park, California, London, Amsterdam, Don Mills, Ontario, Sidney, 1979.
Linz, Peter: An introduction to formal languages and automata, Fourth edition, Jones and Bartlett Publishers 2006.
Martín-Vide, Carlos, Mitrana, Victor and Păun, Gheorghe (eds.) Formal Languages and Applications, Springer, Berlin, 2004.
Révész, György E.: Introduction to Formal Languages, McGraw-Hill, New York, St Louis, San Francisco, Auckland, Bogota, Hamburg, Johannesburg, London, Madrid, Mexico, Montreal, New Delhi, Panama, Paris, Sao Paulo, Singapore, Sydney, Tokyo, Toronto, 1983.
Rozenberg, Grzegorz and Salomaa, Arto (eds.): Handbook of Formal Languages, 3 volumes, Springer, Heidelberg, 1997.
Salomaa, Arto: Formal Languages, Academic Press, New York, London, 1973.